opis
tu:
| | x | | y | | z | |
Napisac rownanie plaszczyzny π przechodzacej przez prosta l1: |
| = |
| = |
| i |
| | 4 | | −2 | | 3 | |
prostopadłej do plaszczyzny π: 3x − y + 2z − 5 = 0
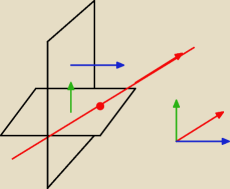
trzeba znaleźć wektor zielony, z iloczynu wektorowego:
przy plaszczyznach: wektor normalny − to wektor prostopadly do niej (zielony − szukany)
plaszczyzna przechodzi przez prostą (prosta ma wektor kierunkowy − rownolegly do niej)
czyli wektor czerwony to (z rownania kanonicznego: [4,−2,3], punkt P
0(0,0,0)
niebieskie: [3,−1,2] (bo 3x, bo −1y, bo 2z)
szukany: zielony, czyli z iloczynu wektorowego:
c
−> = z
−> x n
−> =
|i
−> j
−> k
−>|
| 4 −2 3 |
| 3 −1 2 |
= (jak sie nie pomylilem) = [−1, 1, 2]
A = −1
B = 1
C = 2
P
0(0,0,0)
−1(x−0) + 1*(y−0) + 2*(z−0) = 0
−x+y + 2z = 0 << to trzeba bylo znaleźć
