współczynnik An w szeregu Fouriera
Jarek:
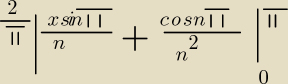
rozwinąć w szereg fouriera funkcję f(x)=IxI dla x∊<−π,π> Mam problem przy końcu, wychodzi mi
wyrażenie powyżej i nie wiem jak dalej je przekształcić
27 cze 19:43
Jarek: sory, pomyliłem się w rysunku, tam miało być xsinx/n oraz cosnx/n2
27 cze 20:06
PW: Coś mi sie kojarzy, że dla funkcji parzystej współczynniki mają postać
a więc po scałkowaniu
| | 2 | | xsinnx | | cosnx | |
|
| ( |
| + |
| )| 0π |
| | π | | n | | n2 | |
− wygląda, że współczynniki policzone poprawnie. A z własności funkcji sinus wynika, że
pierwszy składnik zeruje się, bo sinnπ=0 i sin0=0, natomiast z własności funkcji cosinus
wynika, że
cosnπ=−1 lub cos nπ=1 (na przemian) i cosn•0=1.
Zostaną więc tylko nieparzyste współczynniki
| | 2 | | −2 | | −4 | 1 | |
|
| • |
| = |
|
| , n=1,2,3,... |
| | π | | (2n−1)2 | | π | (2n−1)2 | |
28 cze 00:10
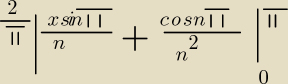 rozwinąć w szereg fouriera funkcję f(x)=IxI dla x∊<−π,π> Mam problem przy końcu, wychodzi mi
wyrażenie powyżej i nie wiem jak dalej je przekształcić
rozwinąć w szereg fouriera funkcję f(x)=IxI dla x∊<−π,π> Mam problem przy końcu, wychodzi mi
wyrażenie powyżej i nie wiem jak dalej je przekształcić