Całka Grzesiek: Całki pomoże ktoś? potrzebuje obliczyć taką całkę:

	x+4
Całka z		dx
	√3 − x2 − 2

i eraz nawet nie wiem jak sie za nią zabrać czy podstawiac t = 1−x² czy obliczać jak wymierne

Mila: Jeśli pod pierwiastkiem jest: 3−x²−2 to rozbij na dwie całki

	x		4
∫		dx+∫		dx
	√1−x2		√1−x2

Grzesiek: faktycznie... czemu ja o tym nie pomyślałem... chyba zmęczenie sesją sie odbija

Mila:

Grzesiek: mam jeszcze jedno zadanie: obliczyć pole obszaru ograniczonego przez krzywe... y=2x²−4x−1 y=−x²+2x−1 całka −x²+2x−1−2x²+4x+1=całka −3x²+6x=−całka3x²+6x t=3x² dt=6x dx = − całka t = −¹₂t² =−^{1₂ 9x⁴ całka ograniczona od 0 do 3 (tak wychodzi z wykresu czyli −4¹₂ * 3⁴ − 0 = − 364,5 i w tym momencie wiem że to zły wynik...

Grzesiek: ju chyba wiem tam powinienem to rozbić na dwie całki

Grzesiek: tam powinno być −3całki z x² + 6 całek z x = −3 * ¹₃ x³ + 6*¹₂x² = −³₃ *3³ + ⁶₂3²=−27+27 = 0 czyli też źle...

Mila: 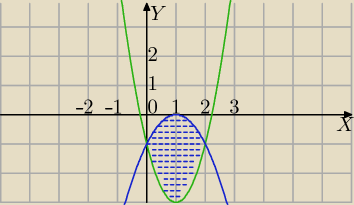y=2x²−4x−1 y=−x²+2x−1 Granice całkowania: 2x²−4x−1=−x²+2x−1 3x²−6x=0 3x(x−2)=0 x=0 lub x=2 ₀∫²(−x²+2x−1−(2x²−4x−1))dx=₀∫²(−3x²+6x)dx=[−x³+3x²]₀²= =−2³+3*2²−0=−8+12=4

Grzesiek: znowu taki głupi błąd... źle oznaczyłęm granice całkowania...