Zaznacz na płaszczyźnie współrzędnych zbiory punktów. wajdzik: Zaznacz na płaszczyźnie współrzędnych zbiory punktów, których współrzędne spełniają poniższe nierówności. |x+y|+|x−y|≤5 dla x≥0 i y≥0 x+y+x−y≤5 2x≤5 dla x≥0 i y<0 x+y−x+y≤5 2y≤5 dla x<0 i y≥0 −x−y+x−y≤5 −2y≤5 dla x<0 i y<0 −x−y−x+y≤5 −2x≤5

	5
x≤
	2

	5
y≤
	2

	5
y≥−
	2

	5
x≥−
	2

Teraz muszę to zaznaczyć w układzie współrzędnych i wyznaczyć część wspólną tak?

Piotr: Moim zdaniem to sume zrobić, gdyż robisz przypadki, ze x≥0 i y≥0 lub x≥0 i y<0 itd

wajdzik: ok, w sumie masz rację, dzięki.

Piotr: Nie wiem czy dobrze to rozwiazałeś, bo np. dla x≥0 i y<0 przyjales ze to jest wartość dodatnia: a przeciez y>x i bedzie juz ujemna ta wartość co wiaze sie ze zmiana znakow

wajdzik: nie pomyślałem o tym.

wajdzik:

	5
Wracając do przykładu który podałeś, nie rozumiem pewnej rzeczy. Napisałem, że y≤		.
	2

Napisałem wcześniej, że y<0 więc zmieniłem znaki z wartości bezwzględnej.

pigor: ..., proponuje tak : |x+y|+|x−y|² ≤ 5 /² ⇔ (x+y)²+2|x+y||x−y|+(x−y)² ≤ 5² ⇔ ⇔ x²+2xy+y²+2|(x+y)(x−y)|+x²−2xy+y² ≤ 5² ⇔ 2x²+2y²+2|x²−y²| ≤ 5² ⇔ ⇔ (2x²+2y²+2x²−2y² ≤ 5² i x²−y² ≥0) lub (2x²+2y²−2x²+2y² ≤ 5² i x²−y²< 0) ⇔ ⇔ (4x²≤5² i |y|≤|x|) lub (4y²≤5² i |y| >|x|) ⇔ (2|x|≤5 i |y|≤|x|) lub (2|y|≤5 i |y|>|x|) ⇔ ⇔ (|x|≤2,5 i |y|≤|x|) lub (|y|≤2,5 i |y|>|x|) ⇔ (|x|≤2,5 i |y|≤|x|) lub (|y|≤2,5 i |x|< |y|) ⇔ ⇔ (−2,5 ≤ x ≤ 2,5 i −|x| ≤ y ≤ |x| ) lub (−2,5 ≤ y ≤ 2,5 i −|y|< x < |y|) . ...

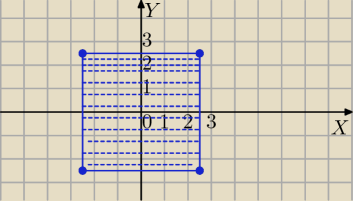
Mila: Dołączam ilustrację.

wajdzik: dzięki wielkie Pigor, postaram się używać tego sposobu. Mila, taki sam rysunek mi wyszedł.