 1) jak to jak ... y=x ... prosta przechodząca przez (0,0) i nachylona pod kątem 45o
y = √x to także jeden ze standardowych wykresów
2) jest 'procedura' rozwiązywania −−− znajdź ją i zastosuj ... jak będziesz miał problemy to
przyjdź z konkretnym pytaniem
3) no i w czym jest problem
1) jak to jak ... y=x ... prosta przechodząca przez (0,0) i nachylona pod kątem 45o
y = √x to także jeden ze standardowych wykresów
2) jest 'procedura' rozwiązywania −−− znajdź ją i zastosuj ... jak będziesz miał problemy to
przyjdź z konkretnym pytaniem
3) no i w czym jest problem  narysuj sobie ten trójkąt ... jedną zmienną 'parametryzujesz'
drugą i 'jedziesz'
4)
y' + y = 0
dy/dx = −y
narysuj sobie ten trójkąt ... jedną zmienną 'parametryzujesz'
drugą i 'jedziesz'
4)
y' + y = 0
dy/dx = −y
| dy | ||
− | = dx | |
| y |
 A więc tak.
1) Wyszło mi do obliczenia ∫ w granicach od 0 do 1 (√x−x)dx
I teraz rozbiłem to na 2 całki ∫(√xdx − ∫xdx=2/3*x(3/2) − x +c.
Jak podstawiłem granicę całkowania to mi wyszło (2/3*1(3/2)−1)−0 i wynik wyszedł mi ujemny
−1/3.
Więc coś mam nie tak.
2) Obliczyłem f'x=2x−6y
f'y=8−6x
Przyrównałem do 0.
2x−6y = 0
8−6x = 0
Z drugiego mi wyszło że x=4/3
Podstawiłem do 1 wzoru i wyszło y=4/9.
Nie wiem czy mam dobrze i teraz jakoś trzeba wyznacznik policzyć.
Więc policzyłem:
f''xx=2
f''yy=0
mieszane wyszły −6 oby dwie czyli dobrze.
W=−36.
Powiedz mi czy dobrze to liczę i co dalej?
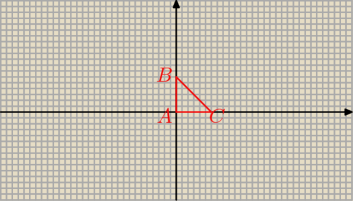
3) No właśnie narysowałem trójkąt tak jak na rysunku jednak nie wiem jak to podstawić do tej
całki.
4) Kompletnie nie umiem.
A więc tak.
1) Wyszło mi do obliczenia ∫ w granicach od 0 do 1 (√x−x)dx
I teraz rozbiłem to na 2 całki ∫(√xdx − ∫xdx=2/3*x(3/2) − x +c.
Jak podstawiłem granicę całkowania to mi wyszło (2/3*1(3/2)−1)−0 i wynik wyszedł mi ujemny
−1/3.
Więc coś mam nie tak.
2) Obliczyłem f'x=2x−6y
f'y=8−6x
Przyrównałem do 0.
2x−6y = 0
8−6x = 0
Z drugiego mi wyszło że x=4/3
Podstawiłem do 1 wzoru i wyszło y=4/9.
Nie wiem czy mam dobrze i teraz jakoś trzeba wyznacznik policzyć.
Więc policzyłem:
f''xx=2
f''yy=0
mieszane wyszły −6 oby dwie czyli dobrze.
W=−36.
Powiedz mi czy dobrze to liczę i co dalej?
3) No właśnie narysowałem trójkąt tak jak na rysunku jednak nie wiem jak to podstawić do tej
całki.
4) Kompletnie nie umiem.
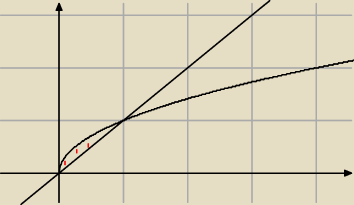 Pierwsze.
Obszar, który masz policzyć, to ten z czerwonymi kreskami. Zauważ (oblicz):
x∊[0,1]
y∊[x,√x]
I albo liczysz całkę: ∫10 dx ∫√xx dy= ∫10
Pierwsze.
Obszar, który masz policzyć, to ten z czerwonymi kreskami. Zauważ (oblicz):
x∊[0,1]
y∊[x,√x]
I albo liczysz całkę: ∫10 dx ∫√xx dy= ∫10
| 2 | 1 | |||
(√x−x)dx= | x32− | x2]10=
| ||
| 3 | 2 |
| 2 | 1 | 4 | 3 | 1 | |||||
− | = | − | = | ||||||
| 3 | 2 | 6 | 6 | 6 |

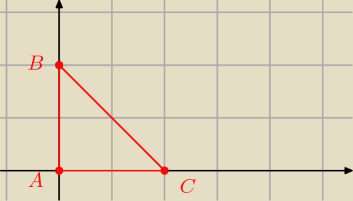 Trzecie.
Widać, że:
x∊[0,1]
prosta BC: y=−x+2
y∊[0,−x+2]
Trzecie.
Widać, że:
x∊[0,1]
prosta BC: y=−x+2
y∊[0,−x+2]
| 1 | ||
I=∫10 dx ∫−x+20 (2−x−y)dy= ∫10[ (2−x)(−x+2)− | (2−x)2 ] dx=
| |
| 2 |
| 1 | 1 | 1 | ||||
∫10 [ (2−x)2− | (2−x)2 ]dx= ∫10 | (2−x)2 dx = ∫10(2−2x+ | x2)dx=
| |||
| 2 | 2 | 2 |
| 1 | 1 | 7 | ||||
−x2+ | x3]10+2=−1+ | +2= | ||||
| 6 | 6 | 6 |
| dy | ||
y'+y=0 ⇔ | =−dx
| |
| y |
| dy | ||
∫ | =−∫dx
| |
| y |