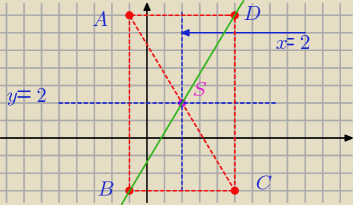
 Dane są przeciwległe wierzchołki kwadratu A=(−1,7) C=(5,−3)
a) wyznacz równanie okręgu opisanego na tym kwadracie
b) wyznacz równanie prostej, w której zawarta jest przekątna BD tego kwadratu
Dane są przeciwległe wierzchołki kwadratu A=(−1,7) C=(5,−3)
a) wyznacz równanie okręgu opisanego na tym kwadracie
b) wyznacz równanie prostej, w której zawarta jest przekątna BD tego kwadratu
| −1+5 | 7−3 | |||
S|AC|= | , | )=(2,2) | ||
| 2 | 2 |
| |AC| | 2√34 | |||
r= | = | =√34 | ||
| 2 | 2 |
| 5 | ||
a= | ||
| 3 |
| 5 | ||
5* | +b=7 | |
| 3 |
| 25 | ||
b=7− | ||
| 3 |
| 4 | ||
b=− | ||
| 3 |
| 5 | 4 | |||
y= | x− | |||
| 3 | 3 |
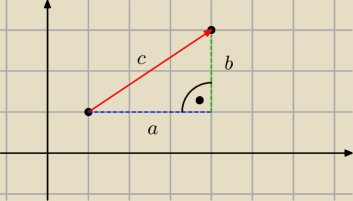 wektor F→ = [a,b]
długość wektora F{→} = |F{→}| :
c2 = a2 + b2
|F{→}| = √a2 + b2
wektor F→ = [a,b]
długość wektora F{→} = |F{→}| :
c2 = a2 + b2
|F{→}| = √a2 + b2
 kwadrat ma wszysktkie boki rowne >
Teraz tak . Akuratnie w tym zadaniu aby napisac rownanie prostej zawierajacej przekatna BD nie
ma potrzeby wyznaczania wspolrzednych punktow B i D . Trzeba tyklko zauwazyc ze w kwadracie
przekatne przecinaja sie pod katem prostym i przecinaja sie w polowie
Srodek odcinka |AC| masz wyznaczony . Wyznacz wspolczynnik kierunkowy prostej AC i potem
napisz rownanie prostej prostopadlej do prostej AC i przechodzacej przez punkt S
kwadrat ma wszysktkie boki rowne >
Teraz tak . Akuratnie w tym zadaniu aby napisac rownanie prostej zawierajacej przekatna BD nie
ma potrzeby wyznaczania wspolrzednych punktow B i D . Trzeba tyklko zauwazyc ze w kwadracie
przekatne przecinaja sie pod katem prostym i przecinaja sie w polowie
Srodek odcinka |AC| masz wyznaczony . Wyznacz wspolczynnik kierunkowy prostej AC i potem
napisz rownanie prostej prostopadlej do prostej AC i przechodzacej przez punkt S
| y2−y1 | ||
Wspolczynnik kierunkowy prostej AC wyznacz albo ze wzoru a= | ||
| x2−x1 |
| −10 | 5 | |||
=− | i dzialaj dalej | |||
| 6 | 3 |

| y2−y1 | −3−7 | 5 | ||||
a= | = | =− | ||||
| x2−x1 | 5+1 | 3 |
| 5 | ||
− | *a2=−1 | |
| 3 |
| 3 | ||
y= | +b | |
| 5 |
| 3 | |
*2+b=2 | |
| 5 |
| 4 | ||
b= | ||
| 5 |
| 3 | 4 | |||
y= | x+ | |||
| 5 | 5 |



