ekstremum analizax2: znajdź ekstrema lokalne funkcji f(x)= (3−x²)e^x D: x:R teraz liczę pochodną, wychodzi mi f'(x)=e^x(−2x+3 − x²) przyrównuję do zera e^x(−x²−2x+3)=0 e^x=0 \/ −x²−2x+3=0 delta = 16 x1=1 x2=−3 i tu moje pytanie, co mam zrobić z tym e^x ? ile musi się tu równać x żeby e wyszło 0 ? nie ma chyba takiej liczby

analizax2: może mi ktoś powiedzieć co mam zrobić z tym e^x ?

ICSP: e^x = 0 ⇒ równanie sprzeczne

analizax2: i mam to całe e^x po prostu pominąć w dalszej części zadania ? czy na tym etapie zakończyć ? w kalkulatorze extremów wychodzi że nie ma ekstremów a kontynuując to zadanie to mam dziedzine x:(−∞,−3)u(−3,1)u(1,+∞) na x:(−∞,−3) f'(x) <0 na x: (−3,1) f'(x)>0 na x: (1,+∞)) f'(x)>0 więc x=−3 minimum lokalne x=1 maksimum lokalne

ICSP: na x > 1 mamy f'(x) < 0 Policz jeszcze wartości ekstremów.

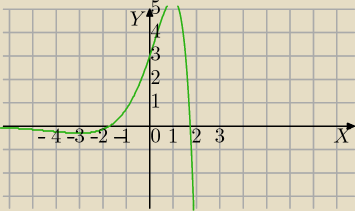
Mila: f(x)=(3−x²)e^x f'(x)=−2x*e^x+(3−x²)e^x f'(x)=e^x*(−2x+3−x²) f'(x)=0⇔−x²−2x+3=0⇔x=−3 lub x=1 f'(x)>0⇔ x∊(−3,1)⇔funkcja rosnąca dla x∊(−3,1) f'(x)<0 ⇔x<−3 lub x>1⇔funkcja malejaca dla x<−3 lub x>1⇔

	−6
dla x=−3 funkcja ma minimum lokalne ymin=
	e3

dla x=1 ma maksimum lokalne y_max=2e

analizax2: oczywiście, na x>1 jest f'(x) < 0, mam tak nawet w zeszycie zapisane ale jak to w brzmiała część zadań z polskiego w podstawówce, wdarł mi się jakiś chochlik dla x=−3 funkcja osiąga minimum równe −6e⁻³ dla x=1 funkcja osiąga maksimum równe 2e² i teraz jeżeli wartości ekstremów dobrze policzyłem to zadanie jest wykonane poprawnie ? mam problem z tymi ekstremami

analizax2: dzięki ICSP i dzięki Mila w x=1 maksimum jest rzeczywiście równe 2e bez kwadratu

Mila: