Równanie trygonometryczne fdf: Rozwiąż równanie 2cos²alfa + 3sin alfa = 0

Mila: 2cos²x+3sinx=0 2(1−sin²x)+3sinx=0 2−2sin²x+3sinx=0 /*(−1) 2sin²x−3sinx−2=0 sinx=t i t∊<−1,1> 2t²−3t−2=0 Δ=9+4*2*2=25

	3−5		−1		3+5
t1=		=		lub t2=		=2∉D
	4		2		4

	−1
sinx=
	2

	π		π
x=		+π+2kπ lub x=2π−		+2kπ
	6		6

	7		11
x=		π+2kπ lub x=		π+2kπ
	6		6

fdf: dzięki wielkie

Mila:

Marysia: tg3x=0 coś mnie zablokowało, pomóżcie

Marysia: i tym rozwiązaniu od Mili, nie bardzo rozumie zapis dwoch ostatnich wierzy, skad jest x1=pi/6+pi i drugi x: 2pi−pi/6 chyba nie kumam

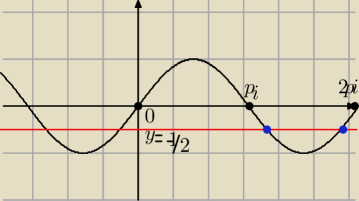
Teraz wielomiany : Teraz widac ? czarny to y=sin(x)

	1
czerwony to y=−
	2