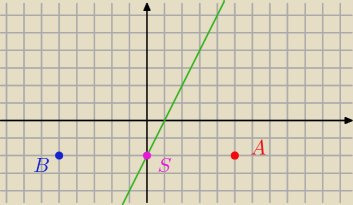
Geometria analityczna bezendu: y=2x−2 y=2*0−2 y=−2 S=(0,−2)

5+xb		−2+yb
	=0 /2		=−2 /2
2		2

5+x_b=0 −2+y_b=−4 x_b=−5 y_b=−2 B=(−5,−2) Czy lepiej obliczyć długość odcinak AS i odłożyć taką samą długość po przeciwnej stronie ? Jeszcze w tablicach mam taki wzór symetria względem osi OY= A=(x,y) A'=(−x,y) ?

bezendu: Polecenie: Dana jest prosta l o równaniu y=2x−2 i punkt A=(5,−2) Wyznacz współrzędne punktu B symetrycznego do punktu A względem prostej l

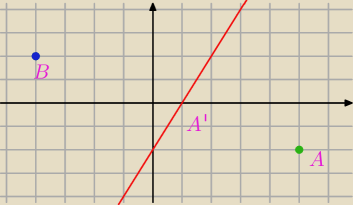
asdf: Masz punkt A: A(5,−2), A =(ax₀, ax₁) znajdź rzut A na prostą l (np. z iloczynu skalarnego), będziesz miec wspolrzedne: A' = (ax₁,by₁) później aby określić B(bx₀,by₀) musisz skorzystać ze wzoru:

	ax0 + bx0
ax1 =
	2

	ay0 + by0
ay1 =
	2

asdf: tam powinno być: A(5,−2), A = (ax₀, ay₀) A' = (ax₁, ay₁) B = (bx₀, by₀)

asdf: zaznaczysz sobie te wspolrzene na ukladzie to zauwazysz.

5-latek: Wiesz co to jest symetria osiowa ? dlaczego wyznaczyles wspolrzedne punktu B jakby osia symetrii byla os OY a nie prosta o danym rownaniu . njpierw wyznacz rownanie prostej ptostopadlej do danej prostej i przechodzacej przez punkt A i potem juz wiesz co dalej

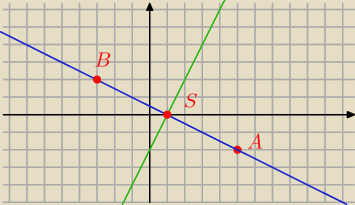
bezendu: prosta prostopadła do prostej y=2x−2

	1
y=−		x+b
	2

punkt A=(5,−2)

	1
−		*5+b=−2
	2

	5		1
−2+		=
	2		2

	1		1
2x−2=−		x+
	2		2

	1		1
2x+		x=		+2
	2		2

5		5
	x=
2		2

x=1 y=2*1−2=0 S=(1,0) środek odcinka AB

5+xb		−2+yb
	=1 /2		=0 /2
2		2

5+x_b=2 −2+y_b=0 x_b=−3 y_b=2 B=(−3,2) teraz się wszystko zgadza ?

5-latek: . Zobacz tez tutaj https://matematykaszkolna.pl/strona/885.html poza tym jest wzor na prosta przechodzaca przez dowolny punkt P(x₀,y₀) y−y₀=a(x−x₀) zapamietaj go masz a=−0,5 to rownanie tej prostej prostopadlej bedzie y+2=−0,5(x−5)to y+2=−0,5x+2,5 to kierunkowa y=−0,5x+0,5 lub ogolna y+0,5x−0,5=0 powinno byc ok.

bezendu: Czyli wszystko się zgadza