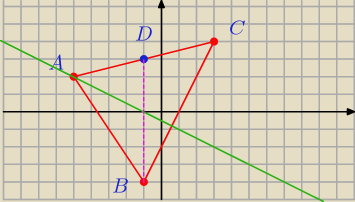
Geometria analityczna Kostek: Dany jest trójkąt o wierzchołkach A=(−5,2) B=(−1,−4) C=(3,4) a) wyznacz równanie prostej, w której zawarta jest wysokość poprowadzona z wierzchołka A b) oblicz długość środkowej BD a) −a+b=−4 /(−1) 3a+b=4 a−b=4 3a+b=4 4a=8 a=2 b=−2 y=2x−2 prosta prostopadła do prostej y=2x−2 i przechodząca przez punkt A

	1
y=−		x+b
	2

	1
−		*(−5)+b=2
	2

	1
b=−
	2

	1		1
y=−		x−
	2		2

b) S_|AC|=(−1,3) |BD|=√(−1+1)²+(3−4)²=1 ok ?

Rafał28: |BD| = 7 Poza tym wszystko OK.

Kostek: a jak zrobić to zadanie na wektorach ?

PW:

	1		1
(1) AD→=		AC→=		[3+5,4−2]=[4,1]
	2		2

Jeżeli oznaczyć D=(x_D,y_D), to (2) AD^→=[x_D+5,y_D−2], a więc z (1) i (2) wynika [x_D+5,y_D−2]=[4,1], skąd x_D=4−5, y_D=1+2, czyli x_D=−1, y_D=3 D=(−1,3) Środkowa BD ma długość równą długości wektora BD^→ |BD|=|BD^→|=√(−1−(−1))²+(3−(−4))²=7. Żeby "na wektorach" rozwiązać część a) należy wziąć dowolny punkt P=(x,y) na szukanej prostej i zauważyć, że AP^→⊥BC^→, a więc iloczyn skalarny tych wektorów jest równy 0: [x+5,y−2]•[3+1,4+4]=0 − otrzymamy równanie prostej.

Kostek: Dziękuje tylko mam jeszcze pytanie jak mam dwa punkty np A=(5,2) C=(3,8) to jak wyznaczyć za pomocą wektorów równanie prostej przechodzącej przez te punkty ?

pigor: ..., np. tak : AB^→= [3−5,8−2]= [−2,6]= −2[1,−3] , więc np. u^→= [1,−3] − wektor kierunkowy prostej AB i punkt A=(5,2)∊AB i jeśli P=(x,y) ≠ A − bieżący punkt prostej AB , to AP^→= [x−5,y−2] , a z warunku równoległości wektorów AP^→||u^→ masz :

x−5		y−2
	=		− równaniekanoniczneprostej przez 2 punkty
1		−3

z którego łatwo przejść do postaci parametrycznej tej prostej (b. przydatnej i wygodnej) ⇔ 1*(y−2)= −3(x−5) ⇔ y−2= −3x+15 ⇔ ⇔ 3x+y−17=0 − szukane równanie prostej AB w postaci ogólnej −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− gdzie n^→=[3,1] − wektor normalny tej prostej i w ten sposób tyle ważnych rzeczy związanych z prostą w 2D "sprzedałem ci tu i ... teraz

Kostek:

pigor: ... zapomniałem dodać do swojego postu ... Amen dla postaci kierunkowej prostej już na poziomie gimnazjum; a najlepiej , to ja ja bym "zabronił" jej stosowanie w szkole średniej .

pigor: ..., oczywiście krótko, moje rozwiązanie wyglądałoby tak : AB^→= [1,−3] ⇒ n^→= [3,1] ⇒ 3(x−5)+1(y−2)= 0 ⇔ 3x+y−17=0 − szukane równanie. ...

Mila: wektorowo BC^→=[4,8] AD1⊥BC − (AD1−wysokość) równanie: 4x+8y+C=0 opisuje wszystkie proste prostopadłe do wektora [4,8] Ponieważ prosta AD1 przechodzi przez punkt A, to wyznaczymy wsp. C 4*(−5)+8*2+C=0 −20+16+C=0⇔C=4 prosta AD1: 4x+8y+4=0

pigor: ..., Dany jest trójkąt o wierzchołkach A=(−5,2), B=(−1,−4) , C=(3,4) a) wyznacz równanie prostej, w której zawarta jest wysokość poprowadzona z A . −−−−−−−−−−−−−−−−−−−−−−−−−−−−− ..., lub tak : BC^→= [4,8]= 4[1,2] ⇒ n^→= [1,2] i A=(−5,2) − wektor normalny i punkt prostej zawierającej wysokość h_BC z punktu A, czyli prostej h_BC: 1(x+5)+2(y−2)=0 ⇔ x+5+2y−4= 0 ⇔ x+2y+1= 0 . ...