Geometria analityczna kostek :

	2
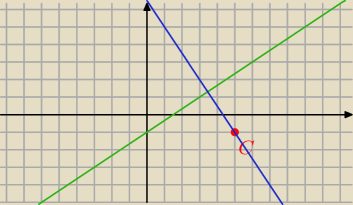
Podstawa AB trójkąta ABC jest zawarta w prostej o równaniu y=		x−1. Wyznacz równanie
	3

prostej, w której zawarta jest wysokość CD tego trójkąta, jeśli wiadomo, że C=(5,−1)

2
	*a=−1
3

	3
a=−
	2

	3
−		*5+b=−1
	2

	15
b=−1+
	2

	13
b=
	2

	3		13
y=−		x+
	2		2

zgadza się ?

vitek1980:

kostek : Dany jest kwadrat o przeciwległych wierzchołkach A=(−6,2) i C=(4,−4). Wyznacz długość promienia okręgu wpisanego w ten kwadrat. |AB|=√(4+6)²+(−4−2)²=2√34 d=2√34 a=a√2 a√2=2√34

	2√34		√2		4√17
a=		*		=		=2√17
	√2		√2		2

	a		2√17
r=		=		=√17
	2		2

kostek : chochlik |AC|

5-latek: Kostek moze zapamietaj sobie tez taki wzor . Rownanie prostej przechodzacej przez dowolny punkt P(x₀,y₀) ma postac y−y₀=a(x−x₀) gdzie a to wspolczynnik kierunkowy prostej

	3
jesli wyznaczyles a=−		to podsatwiasz do wzoru i masz rownnaie prostej czyli
	2

y+1=−1,5(x−5) to y=−1,5x+6,5(kierunkowa) i z kierunkowej masz ogolna y+1,5x−6,5=0

kostek : Dziękuje

kostek : Oblicz pole koła wpisanego w kwadrat o kolejnych wierzchołkach A=(5,1) B=(7,−3) |AB|=√(7−5)²+(−3−1)²=√20=2√5 2r=a

	2√5
r=		=√5
	2

P=πr² P=5π czy lepszy zapis P=15,7

kostek : Oblicz pole koła wpisanego w kwadrat o kolejnych wierzchołkach A=(5,1) B=(7,−3) |AB|=√(7−5)²+(−3−1)²=√20=2√5 2r=a

	2√5
r=		=√5
	2

P=πr² P=5π czy lepszy zapis P=15,7

5-latek: lepszy jest 5π. Mozesz tez zauwazyc ze dlugosc odcinka |AB| to dlugosc wektora AB→. Bede pisac bez strzalki (ale nalezy pisac ) masz dwa punkty A(5,1) i B(7,−3) to wektor AB[7−5 −3−1] to AB[2,−4] Teraz dlugosc tego wektora AB to |AB|=√2²+(−4)²=√20= 2√5 Poucz sie wektorow . Bedzie latwiej rozwiazywac zadania z geometrii analitycznej