druga pochodna agusia229: obliczyc druga pochodna z f(x) = 2ln x +x² w którym miejscu ta funkcja jest wypukła w którym wklęsła

Bogdan: to może sama wyznacz drugą pochodną i podaj wynik

agusia229:

	2
f(x) ' =		+ 2x
	x

	−2
f(x) '' =		+2
	x2

Bogdan:

	2x2 − 2		2(x − 1)(x + 1)
f''(x) =		⇒ f"(x) =		i x≠0
	x2		x2

Jaki znak przyjmuje druga pochodna funkcji w przedziale, w którym jest wypukła?,a jaki znak w przedziale, w którym jest wklęsła?

agusia229: dobrze ta pochodna? ta druga ma byc wieksza od 0 to wtedy jest wypukła a jak jest mniejsza od zera to wklęsła

Bogdan:

−2		−2 + 2x2		2(x2 − 1)		2(x − 1)(x + 1)
	+ 2 =		=		=
x2		x2		x2		x2

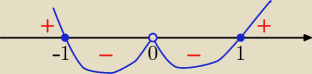
Jeśli omówimy się, że funkcja jest w przedziale wypukła, gdy f''(x) > 0, jest wklęsła gdy f''(x) < 0, to odczytaj z rysunku przedziały wypukłości i wklęsłości.

agusia229: to przekształcenie zrozumialam tylko pytałam czy ja dobrze ją obliczyłam czyli wypukła jest od (−nieskonczonosci, −1) i od (1; +nieskonczonosci) a wklesla od (−1;1) − {0}

agusia229: f(x,y) = cos (x2 + 3y2) obliczyć drugą pochodną... do tego nie umiem sie zabrac bo nie mamy takich przykladow rozwiazanych..

Bogdan: Pochodne dobrze obliczyłaś. Pytanie "dobrze ta pochodna?" było niejasne. Łącznik i w sformułowaniu "wypukła jest od (−nieskończoności, −1) i od (1; +nieskończoności) jest tutaj niewłaściwy. Bezpieczniej jest tak: funkcja jest wypukła dla x∊(−∞, −1), (1, +∞) funkcja jest wklęsła dla x∊(−1, 0), (0, 1)

agusia229: dziekuje a potrafisz rozwiazac to f(x,y) albo mozesz dac jakas wskazówkę?

agusia229: f(x,y) = cos (x² + 3y²) obliczyć drugą pochodną

Bogdan: f(x, y) = cos(x² + 3y²) Oblicz najpierw pochodną funkcji g(x) = cos(x² + a) oraz funkcji h(y) = cos(b + 3y²)

agusia229: g(x)' = −sin (x² +a) nie no nie wiem co dalej ... jakos przez podstawianie ?

Bogdan: g'(x) = −sin(x² + a) * 2x = −2x*sin(x² + a), czyli f'_x(x, y) = −2x*sin(x² + 3y²).

agusia229: h(y)= −sin (b+3y²) * 6y = −6y sin (x²+3y²)

agusia229: i co dalej?

Bogdan: Są pierwsze pochodne: f'_x(x, y) = −2x*sin(x² + 3y²) oraz f'_y(x, y) = −6y*sin(x² − 3y²) Z każdej z nich wyznacz w ten sam sposób kolejne pochodne, po x oraz po y

agusia229: g(x) = −2x sin 9 (x² +a) g'(x) = −2* (−cos) (x²+a) *2x = 4 x cos (x² +a) h(y) = − 6y sin ( b + 3y²) h'(y) = −6 cos (b +3y²) * 6y = 36 cos (b +3y²) a w f'y (x,y) = −6y sin (x² tu ma byc − czy + w koncu 3y²?