Zaznacz na płaszczyźnie współrzędnych zbiory punktów
wajdzik: Zaznacz na płaszczyźnie współrzędnych zbiory punktów, których współrzędne spełniają podane
układy nierówności.
{3−|y|+2≥0
{|y|<1
I mam teraz pytanie.
Mam tutaj podać 4 rozwiązania czy 2?
Bo mi się pomieszało.
Dla y≥0 i dla y<0 czyli 2. Tak mi się wydaje.
Proszę o odpowiedź.
25 cze 11:35
ZKS:
A nie łatwiej po prostu rozpisać tak
3 − |y| + 2 ≥ 0 ⇒ |y| ≤ 5 ⇒ −5 ≤ y ≤ 5
|y| < 1 ⇒ −1 < y < 1
i wtedy narysować.
25 cze 11:52
krystek: Masz zaznaczyć na płaszcźnie , rozpatrując jak napisałeś dla y<0 i y≥0
25 cze 11:53
krystek: o już ZKS podał Tobie IIsposób
25 cze 11:54
krystek: Podejrzewam ,że w pieswszej musi być jeszcze x.
25 cze 11:55
wajdzik: Tak, w pierwszym jest 3x−|y|+2≥0, musiało mi uciec.
25 cze 11:58
wajdzik: więc co teraz

3x−|y|+2≥0
−|y|≥−3x−2
|y|≤3x+2
y≤3x+2 V y≥−3x−2
−3x−2≤y≤3x+2
25 cze 12:01
wajdzik: zgadza się?
25 cze 12:01
ZKS:
To zapisujesz
3x − |y| + 2 ≥ 0
|y| ≤ 3x + 2
−3x − 2 ≤ y ≤ 3x + 2
i rysujesz.
25 cze 12:01
ZKS:
Ubiegłeś mnie.

25 cze 12:02
wajdzik:
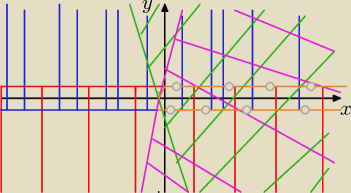
Pomarańczowy kolor to część wspólna, zgadza się?
25 cze 12:22
wajdzik: 
25 cze 12:39
wajdzik: 
25 cze 14:32
wajdzik: 
25 cze 14:41
wajdzik: 
25 cze 16:56
Mila:
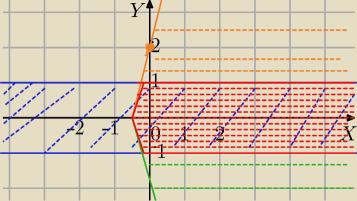 |y|≤1
|y|≤1 punkty między prostymi y=−1 i y=1 i na tych prostych
3x−|y|+2≥0⇔3x+2≥|y|
y≥0
y≤3x+2 punkty leżące pod półprostą (pomarańczową) i y≥0 i na półprostej
y<0
−y≤3x+2⇔
y≥−3x−2 punkty leżące nad półprostą zieloną i y<0 i na półprostej
Rozwiązanie to obszar zaznaczony na czerwono.
25 cze 19:36
Mila: Oj, rozwiązałam:
|y|≤1
Sam skoryguj.
25 cze 19:47
 3x−|y|+2≥0
−|y|≥−3x−2
|y|≤3x+2
y≤3x+2 V y≥−3x−2
−3x−2≤y≤3x+2
3x−|y|+2≥0
−|y|≥−3x−2
|y|≤3x+2
y≤3x+2 V y≥−3x−2
−3x−2≤y≤3x+2

 Pomarańczowy kolor to część wspólna, zgadza się?
Pomarańczowy kolor to część wspólna, zgadza się?




 |y|≤1 punkty między prostymi y=−1 i y=1 i na tych prostych
3x−|y|+2≥0⇔3x+2≥|y|
y≥0
y≤3x+2 punkty leżące pod półprostą (pomarańczową) i y≥0 i na półprostej
y<0
−y≤3x+2⇔y≥−3x−2 punkty leżące nad półprostą zieloną i y<0 i na półprostej
Rozwiązanie to obszar zaznaczony na czerwono.
|y|≤1 punkty między prostymi y=−1 i y=1 i na tych prostych
3x−|y|+2≥0⇔3x+2≥|y|
y≥0
y≤3x+2 punkty leżące pod półprostą (pomarańczową) i y≥0 i na półprostej
y<0
−y≤3x+2⇔y≥−3x−2 punkty leżące nad półprostą zieloną i y<0 i na półprostej
Rozwiązanie to obszar zaznaczony na czerwono.