Zadanie ostrosłup prawidłowy sześciokatny.
Mucha: Pole ściany bocznej ostrosłupa prawidłowego sześcikątnego jest równe 8 pierwiastków z 6, a
wysokośc tego ostrosłupa ma 8 cm. Oblicz pole.
Ciekawe zadanie.
Prosiłam pare osób, nikt nie rozwiązał tak 'prosto' (tzn. żeby nie wykraczało to poza wiedzę 3
gim)
Ja sama z matmy najgorsza nie jestem ale to zadanie przerasta moje umiejętności.
Tych, co jakiś pomysł na rozwiązanie tego zadania proszę o kontakt: GG:6413768
Pozdrawiam
22 wrz 22:16
Bogdan:
Pole czego trzeba obliczyć?
22 wrz 22:32
nalepek:
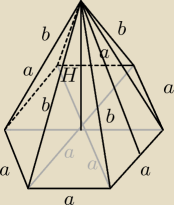
PΔ=8
√6
H=8
PΔ=
a*h2
8
√6=
a*h2 /*2
16
√6=a*h
h
2+(
12a)
2=b
2
H
2+a
2=b
2
16
√6=a*h
h
2+(
12a)
2=b
2
64+a
2=b
2
16
√6=a*h
dokonczysz ?
23 wrz 00:33
Bogdan:
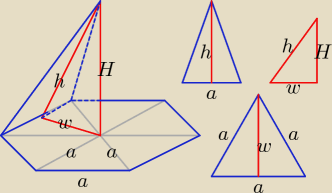
| | 1 | | 3 | |
H = 8, w = |
| a√3, w2 = |
| a2 |
| | 2 | | 4 | |
Układ równań:
2. { w
2 + 8
2 = h
2
1. { ah = 16
√6
Dla ucznia dysponującego wiedzą z gimnazjum taki układ równań może być za trudny.
23 wrz 00:50