Oblicz pole figury ograniczonej krzywymi o równaniach tom: y = x2 − 6x + 10, y = 6x − x2

tom: Oblicz pole figury ograniczonej krzywymi o równaniach y = x2 − 6x + 10, y = 6x − x2

Miś: Napisz to porządnie jeśli oczekujesz pomocy

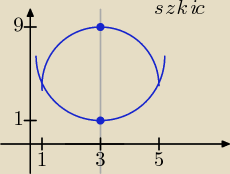
Bogdan: y = x² − 6x + 10, W₁ = (3, 1) y = −x² + 6x, W₂ = (3, 9) x² − 6x + 10 = −x² + 6x ⇒ 2x² − 12x + 10 = 0 ⇒ x² − 6x + 5 = 0, x₁ = 1, x₂ = 5 Pole P = ∫₁⁵ [(−x² + 6x) − (x² − 6x + 10)] dx

natalia: y=x2−3x y=x

natalia: y=x2−3x i y=x

Bogdan: a tu jest mój post z września 2009 , o co natalio trzeba zrobić?

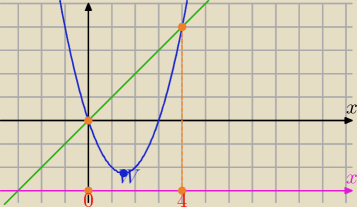
Bogdan: Jeśli chodzi o obleczenie pola między wykresami: y = x² − 3x i y = x, to najpierw wyznaczamy odcięte punktów przecięcia tych wykresów: x₁ = 0, x₂ = 4.

	3		9
Wierzchołek paraboli W =		. −		), dla wygody obliczeń przesuwamy wykresy do
	2		4

góry o np. 3 jednostki, wówczas wykresy przybierają wzory: parabola: y = x² − 3x + 3, prosta y = x + 3. Pole między prostą i parabolą w przedziale <0, 4> jest równe P = ∫₀⁴ (x + 3 − x² + 3x − 3)dx