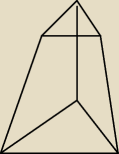
 Poprowadzono płaszczyznę równoległą do podstawy ostrosłupa utworzył się tzw. ostrosłup ścięty.
Wyznacz wzór na objętość ostrosłupa ściętego mając dane pole podstawy dolnej S1 i górnej S2
oraz wysokość h.
Poprowadzono płaszczyznę równoległą do podstawy ostrosłupa utworzył się tzw. ostrosłup ścięty.
Wyznacz wzór na objętość ostrosłupa ściętego mając dane pole podstawy dolnej S1 i górnej S2
oraz wysokość h.
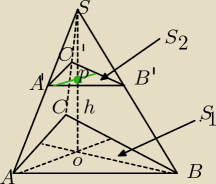 OS=H
OP=h
ΔABC∼ΔA'B'C'
OS=H
OP=h
ΔABC∼ΔA'B'C'
| S1 | ||
k2= | stosunek pól figur podobnych jest równy kwadratowi skali podobienstwa | |
| S2 |
| √S1 | ||
k= | skala podobieństwa, | |
| √S2 |
| H | √S2 | ||
= | ⇔H*√S2−√S2*h=H√S1⇔H*(√S2−√S1=h*√S2 | ||
| H−h | √S1 |
| √S2*h | ||
H= | ||
| √S2−√S1 |
| √S2*h | √S2 | √S2−√S2+√S1 | ||||
H−h= | −h=h*( | −1)=h* | ||||
| √S2−√S1 | √S2−√S1 | √S2−√S1 |
| h*√S1 | ||
H−h= | wysokość odciętego ostrosłupa | |
| √S2−√S1 |
| 1 | h*√S1 | 1 | S1*√S1*h | |||||
Vodciętego o.= | *S1* | = | * | |||||
| 3 | √S2−√S1 | 3 | √S2−√S1 |
| 1 | 1 | √S2*h | ||||
V{ABCS}= | *S2*H= | *S2* | ||||
| 3 | 3 | √S2−√S1 |
| (S2√S2−S1√S1)*h | ||
Vo.ściętego= | ||
| 3(√S2−√S1) |
| h*(S1+S2+√S1*S2) | ||
Vo.ściętego= | ||
| 3 |