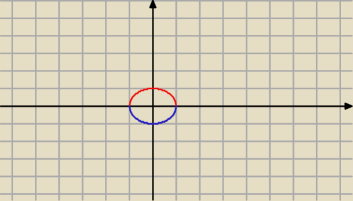
. asdf: wyprowadzenie wzoru na obwód koła.. (x−a)² + (y−b)² = r² niech będzie to okrąg o środku S(0,0) i promieniu 1: x² + y² = 1 ⇒ y² = 1 −x² ⇒ y = √1−x² v y = −√1−x², wezmę pierwsze równanie (na czerwono i pomnożę długość * 2) długość łuku: dl² = dy² + dx² dl = √dy² + dx²

	dy
dl = dx√1 + (		)2
	dx

	dy
dl = √1 + (		)2 dx
	dx

dl = √1 + (y')² dx długość łuku na przedziale <−1,1> : ∫₋₁¹ √1 + (y')² dx

	−x
y' = √1−x2 ' =
	√1−x2

	x2
(y')2 =
	1−x2

	x2		1 − x2 + x2
∫−11 √1 +		dx = ∫−11 √		dx =
	1−x2		1−x2

	1		1
∫−11 √		dx = ∫−11		dx = arcsin ↕/sup>{−1}1 = ...
	1−x2		√1−x2

−−−−−−

	π
arcsin(1) =
	2

	π
arcsin(−1) = −
	2

−−−−−−

	π		π
... =		− (−		) = π
	2		2

obwód okręgu to 2 * długość łuku = 2π a jak teraz udowodnić, że dla każdego r ≥ 0 jest wzór: 2πr?

asdf: tam na końcu powinno być bwód koła (przepraszam )

ZKS: y = ±√r² − x² Długość łuku na przedziale [−r ; r]

	−x
y' =
	√r2 − x2

	x2
(y')2 =
	r2 − x2

	x2
2 * ∫r−r (1 +		)1/2dx =
	r2 − x2

	r
2 * ∫r−r		dx = 2 * πr
	√r2 − x2

asdf: ostatniej równości nie wiem skąd wziąłeś:

	r		dx		x
∫		dx = r ∫		= r*arcsin		+ C, i z tego jak dalej?
	√r2−x2		√r2−x2		r

asdf: .

asdf: ::(

asdf:

ZKS:

	r		x
2 * ∫		dx = [r * arcsin(		]r −r =
	√r2 − x2		r

	π		π
2 * [r * arcsin(1) − r * arcsin(−1)] = 2 * [r *		+ r *		] = 2πr
	2		2

asdf: Już rozumiem..takie to trywialne dzięki bardzo