calka ada: oblicz ∫(na dole calki k) sinxdx, gdzie k jet fragmentem krzywe y=sinx, 0≤x≤π

wredulus_pospolitus: obliczasz całkę z sinx po krzywej sinx

michal: tak. ∫sinx po krzywej y=sinx

wredulus_pospolitus: zdecyduj się co do imienia ... i płci a rozumiesz co oznacza całkowanie po krzywej

ada: ok ok. tak rozumiem. tylko prosilabym rozwiaznaie

wredulus_pospolitus: to w końcu Ada

ada: tak ada. bedziemy pisac o mojej osobie czy o zadaniu?

wredulus_pospolitus: skoro rozumiesz co oznacza całkowanie po krzywej i masz całkowac daną krzywą po tejże własnie krzywej to rozwiązanie powinno być natychmiastowe chyba że własnie nie rozumiesz co oznacza całkowanie po krzywej

ada: a podalbys mi rozwazanie?

wredulus_pospolitus: jasne ... =0

ada: a cale rozwazanie od poczatku do konca...ale dowcipny jestes

wredulus_pospolitus: chyba że (co jest mocno prawdopodobne) coś tutaj pokićkałaś/−eś w treści zadania albo jest to 'chytry' plan wykładowcy, aby sprawdzić w prosty sposób czy rozumiecie ideę całkowania krzywoliniowego

wredulus_pospolitus: no i właśnie widać że nie masz bladego pojęcia co oznacza całkowanie krzywoliniowe dla funkcji jednej zmiennej

ada: czyli bedzie tak ∫(od o do pi)sinx= −cosx]0d zera do pi= −1+1 ?

Artur z miasta Neptuna: Jezeli jest to calka krzywoliniowa po krzywej sinx to NIE jezeli jest to zwykla calka oznaczona to tak

ada: uwazam ze trzeba wykozystac calki podwojne, tylko nie wiem jaki przedzial wziac

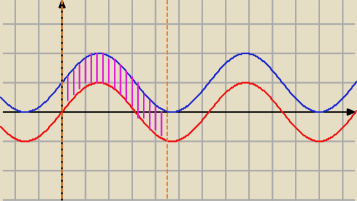
wredulus_pospolitus: jeżeli krzywa jest postaci y(x) = sinx a funkcja podcałkowa to f(x) = sinx tak by wyglądało (obliczanie pola ... fioletowe kreski) gdybyś miał/−a ∫_k (sinx +1) dx po krzywej k:y=sinx w granicach 0:π

wredulus_pospolitus:

	3
a raczej nie 0:π ... tylko 0:		π
	2

0: przedzial na pewno byl od 0:π.

wredulus_pospolitus: nie rozumiesz ... ja podałem inny przykład na innym przedziale aby zademonstrować jaka jest geometryczna intrepretacja całki krzywoliniowej po funkcji jednej zmiennej

ada: czyli zadanie ktore podalam bedzie z wykorszyatniem zwykle calki?

wredulus_pospolitus: napisałem Ci jezeli jest to zwykła całka oznaczona czyli ∫₀^π sinx dx to tak jeżeli jest to całka krzywoliniowa ∫_k sinx dx ; gdzie k:y=sinx dla 0≤π to NIE wyniki będa takie same i będą wynosiły 0 ale chodzi tutaj o interpretacje geometryczną tych dwóch (różnych) całek

wredulus_pospolitus: w zwykłej całce obliczasz pole pomiędzy osią OX a krzywą daną pod całką w drugiej obliczasz pole pomiędzy krzywą po której obliczasz całkę, a krzywą daną pod całką

wredulus_pospolitus: po prostu ... jako zwykła całka ... funkcja podcałkowa ma takie samo pole nad jak i pod osią OX i dlatego całka z niej =0 ale jako całka krzywoliniowa po takiej krzywej ... nie ma W OGÓLE pola ... bo sie pokrywa z krzywą po której (względem której) obliczane jest pole