. Pawexs: Wykaż, że długość promienia okręgu wpisanego w trójkąt prostokątny wyraża się wzorem

	a+b−c
r=
	2

wredulus_pospolitus: rysunek chociaż zrobiony

Pawexs:

	2P		ab		ab
r=		P=		r=
	a+b+c		2		a+b+c

wredulus_pospolitus: z tw. pitagorasa a² + b² = c² −> a² + b² − c² = 0 −> a²+b² + 2ab − c² = 2ab −> (a+b)² − c² = 2ab −>

	ab		2P
−> (a+b−c)(a+b+c) = 2*2*		−> (2p)*(a+b−c) = 4*(P) −> a+b−c =		−>
	2		p

	2P		a+b−c
−> a+b−c =		−> a+b−c = 2r −> r =
	P   r		2

oznaczenia: p −−−− połowa obwodu trójkąta P −−−− pole trójkąta korzystasz ze wzoru: P_Δ = p*r

wredulus_pospolitus: natomiast wzór: P=p*r masz z tego co napisałes powyżej

	2P		a+b+c
r =		−> r*		= P −> r*p = P
	a+b+c		2

Pawexs: Rozumiem! Dzięki

pigor: ..., lub z własności odcinków przyprostokątnych i przeciwprostokątnej tycznych do okręgu masz równość : a−r+b−r = c ⇔ 2r= a+b−c ⇔ r = ¹₂(a+b−c) c.n.w. . ...

Eta:

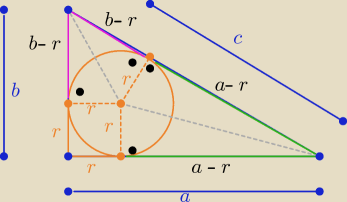
	a+b−c
c= a−r+b−r ⇒ 2r= a+b−c ⇒ r=
	2

pigor: ..., o! jak piknie, a myślałem, że to ja piszę. ... gotowce

Eta: Hejpigor Chciałam tylko zilustrować Twojego "gotowca"