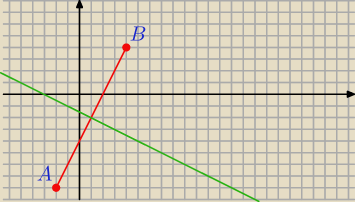
II. Geometria analityczna. lewy: 2. Dane są punkty: A = (−2, −8), B = (4, 4), C = (−3, 5). Wykonaj polecenia: a) znajdź równanie prostej AB, b) znajdź równanie symetralnej odcinka AB, c) znajdź równanie środkowej trójkąta ABC poprowadzonej z wierzchołka

bezendu: a) −2a+b=−8 / *(−1) 4a+b=4 2a−b=8 4a+b=4 6a=12 a=2 4*2+b=4 8+b=4 b=−4 y=2x−4 b) √(x+2)²+(y+8)²=√(x−4)²+(y−4)² (x+2)²+(y+8)²=(x−4)²+(y−4)² x²+4x+4+y²+16y+64=x²−8x+16+y²−8y+16 4x+4+16y+64=−8x+16−8y+16 24y=−12x−36 /24

	1		3
y=−		x−
	2		2

bezendu: c) którego wierzchołka? sprecyzuj

Gustlik: Bezendu, zrobiłeś trochę dookoła swiata. Najprościej wektorami: A = (−2, −8), B = (4, 4), C = (−3, 5) ad a) AB^→=[4−(−2), 4−(−8)]=[6, 12]

	12
a=		=2
	6

y=2x+b podstawiam wsp. np. B: 4=2*4+b 4=8+b b=−4 Odp. y=2x−4 ad b) Współczynnik kier. symetralnej a₂=−U{1]{2} (war. prostopadłości) y=−U{1]{2}x+b A = (−2, −8), B = (4, 4), C = (−3, 5) Liczę środek AB:

	−2+4		−8+4
S=(		,		)=(1, −2)
	2		2

−2=−U{1]{2}*1+b −2=−U{1]{2}+b

	1
b=−1
	2

	1
Odp. y=−U{1]{2}x−1
	2

bezendu: Gustlik masz 100% racji, że wektorami jest prościej ale nie byłem pewny i dlatego zrobiłem ''tradycyjnie''

pigor: ..., Dane są punkty: A = (−2, −8), B = (4, 4), C = (−3, 5). Wykonaj polecenia: a) znajdź równanie prostej AB, b) znajdź równanie symetralnej odcinka AB, −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− no to może jeszcze tak : b) AB^→= [4+2, 4+8]= [6,12]= 6 [1,2] i S_AB=(¹₂(−2+4)),¹₂(−8+4))= (1,−2) ⇒ ⇒ s_AB : 1(x−1)+2(y+2)=0 ⇔ x+2y+3=0 − szukane równanie symetralnej s_AB, wtedy np. tak : a) AB : 2(x−4)−1(y−4)=0 ⇔ 2x−y−4=0 − szukane równanie prostej AB. ...

Gustlik: Pigor, masz rację tylko w szkole nie przerabia się tych "Twoich" wzorów nawet na rozszerzeniu. A szkoda...

pigor: a dlaczego nie może warto pokazać to zainteresowanym uczniom np. tak : jeśli p: Ax+By+C=0 i (x_o,y_o)∊p, czyli Ax_o+By_o+C=0 ⇒ C= −Ax_o−By_o i Ax−Ax_o+By−By_o= 0 ⇒ A(x−x_o)+B(y−y_o)= 0 − równanie prostej przez 1 punkt . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− czy to takie trudne dla obecnych nauczycieli (niech oleją podstawę, czy jak to gawno się nazywa) ; stąd jak znalazł np. A(x−x_o)+B(y−y_o)+C(z−z_o)=0 − równanie płaszczyzny przez 1 punkt w 3D itp. analogie potrzebne na studiach,