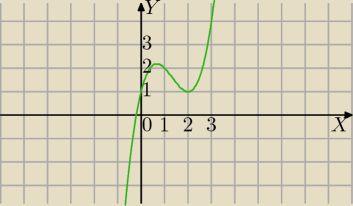
Ekstrema lokalne funkcji Bart: Witam mam takie zadanie: Wyznaczyć ekstrema lokalne funkcji: f(x)=x³−4x²+4x+1 Zrobiłem to tak: [WK] f'(x)=3x²−8x+4 po obliczeniu delty: x₁=2 x₂=6 [WW] f''(x)=6x−8 f''(2)=12−8 4>0 występuje minimum lokalne f''(6)=36−8=28 28>0 występuje minimum lokalne w x=2 minimum lokalne przy f(2)=8−16+8+1=1 w x=6 minimum lokalne przy f(6)=6³−4*36+24+1=97 Moje pytanie czy dobrze jest to zrobione zadanie i dwa czy mogą w jednym takim równaniu wystąpić dwa np minima lokalne? Bo wydaje mi się, że mam błąd. proszę o pomoc. Dzięki!

Bart: odswiezam

Mila: f(x)=x³−4x²+4x+1 f'(x)=3x²−8x+4 f'(x)=0⇔3x²−8x+4=0 Δ=64−4*3*4=16

	8−4		2		8+4
x=		=		lub x=		=2
	6		3		6

Badam znak pochodnej f'(x)>0⇔funkcja jest rosnąca⇔

	2
3(x−		)*(x−2)>0
	3

	2
x<		lub x>2 funkcja rosnąca
	3

	2
dla x∊(		,2) funkcja malejąca
	3

	2		59
w x=		funkcja ma maksimum lokalne y max=
	3		27

	2
( pochodna przy przy przejściu przez punkt		zmienia znak z dodatniego na ujemny ↗↘)
	3

w x=2 funkcja ma min lokalne y_min=1 ( pochodna zmienia znak z ujemnego na dodatni↘↗) albo liczysz wartości II pochodnej:

	2		2
f''(x)=6x−8 , f''(		)=6*		−8=−4<0 maksimum lokalne
	3		3

f''(2)=4 >0 minimum lokalne

Bart: bardzo dziękuje za odpowiedź widze że błędów narobiłem sporo

Mila:

Ajtek: Hej Mila . "Prawie" Ciebie nie widać