Obliczyć pole obszaru całka Kasia: Obliczyć pole ograniczone liniami y=lnx, y=0, x=e

xdc: Zrób wykresy tych funkcji na jednym rysunku zobaczysz, że pole sprowadza się do pola po lnx w graniach od 1 do e więc masz do policzenia całkę oznaczoną ∫^e₁ lnx dx

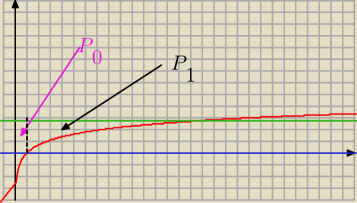
asdf: liczysz układ: y = 0 y = lnx x = 1, widac, ze pole P₀ = podstawa * wysokość = 1 * e = e teraz P₁ rozwiąż układ:

⎧	y=e
⎩	y=lnx

czyli: lnx = e lnx = elne x = lne^e x = e^e masz granicę całkowania od 0 do e^e, z dołu ograniczone przez lnx, z góry przez e, rozwiązujesz: ∫₀^ee [ e − lnx] dx = całka z lnx:

	u = lnx, v' = 1
∫lnxdx =
	1   u' = , v = x   x

∫lnx dx = xlnx −∫dx = xlnx − x ∫e dx = e∫dx = e*x masz więc: ∫₀^ee [ e − lnx] dx = e*x − xlnx + x ||^ee₀ = ...

asdf: poprawka, druga granica całkowania to od 1 do e^e

asdf: źle przeczytałem zadanie...ja zrobiłem takie pole: ograniczone przez: y = lnx y = 0 y = 3 ....

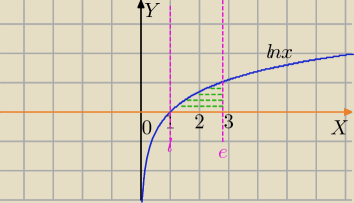
Mila: lnx=0⇔x=e⁰=1 Granice całkowania od 1 do e ₁∫^elnxdx=[xlnx−x]₁²=elne−e−1ln1+1=e−e−0+1=1