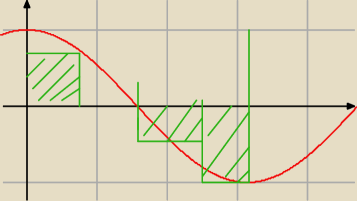
. asdf: całka oznaczona. zadanie: 1. Podać definicje sumy całkowej i wyjaśnić występujące w def. oznaczenia. Obliczyć sumęcałkową dla funkcji f(x) = cos(x) w przedziale <0;π>, jeżeli przedział dzielimy na 4 części, a za punkty pośrednie wybieramy prawe końce przedziałów. (Sporządzić rysunek) zał: funkcja jest ciągła w przedziale <a,b> przedział <a,b> dzielimy na n normalnych podziałów (równej długości), gdzie n∊N oraz zachodzi nierówność: a = x₀ < x₁ < x₂ < ... < x_n = b Δx_i = x_i+1 − x_i, gdzie 1 ≤ i < n.

	1
δn = max(Δxi), a z tego musi wynikać, że limn→∞ δn = 0, bo limn→∞		= 0
	n

za punktu pośrednie w każdym podziale wybieramy takie ξ_i ∊ (x_i, x_i+1) Suma całkowa to suma wszystkich prostokątów, czyli: lim_n→∞∑_i=1ⁿ f(ξ_i)*Δx_i Δx_i − podstawa f(ξ_i) − wysokość teraz mam: f(x) = cosx, w przedziale <0;π> na 4 części, wybierając prawe końce przedziałów, czyli:

	1
Δxi = xi+1 − xi =
	4

	1		π		√2
ξ1 =		π ⇒ f(ξ1) = cos(		) =
	4		4		2

	2		π
ξ2 =		π ⇒ f(ξ2) = cos(		) = 0
	4		2

	3		3π		π		π		2√2
ξ3 =		π ⇒ f(ξ3) = cos(		) = cos(π−		) = −cos(		= −
	4		4		4		4		2

ξ₄ = π ⇒ f(ξ₄) = cos(π) = −1 i jak to teraz będzie, pole to 1?

asdf: kurde.. źle

	π		π		π		π
S = f(ξ1)*		+ f(ξ2)*		+ f(ξ3)*		+ f(ξ4)*		=
	4		4		4		4

π√2		π√2		π√2
	+ 0 − (		) − (−1) =		+ 1?, na pewno nie może wyjść pole ujemne
8		8		4

więc to będzie tyle co napisałem, czy:

	π		π		π		π
S = f(ξ1)*		+ f(ξ2)*		+ f(ξ3)*		+ f(ξ4)*		=
	4		4		4		4

	π√2		π√2
|		+ 0 − (		) + (−1)| = |−1| = 1?
	8		8

asdf: ?

Trivial: Tak trudno sprawdzić licząc całkę w pamięci? ∫₀^π cosxdx = 0.

asdf: no ale tu masz na 4 części..gdzie przy f(ξ₃) = 0 Jakie tu w koncu bedzie rozwiązanie? funkcja f(x) = cosx, podzielona na 4 częsci w przedziale <0;π>, obliczyć pole..wyznaczylem ξ₁,ξ₂,ξ₃,ξ₄, ale pole juz nie wiem jakei bedzie

Nienor: asdf masz granicę z takich przediałów normalnych.

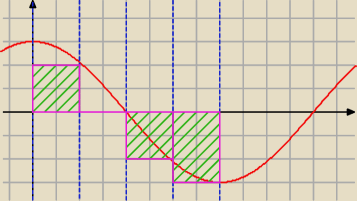
Trivial: Aha, nie doczytałem. Trzeba policzyć dzieląc przedział na 4 kawałki...

	π
σ =		(cos(π/4) + cos(2π/4) + cos(3π/4) + cos(4π/4)) = −1.
	4

Nienor: w definicji oczywiście

Trivial:

	π
σ = ... = −		.
	4

asdf: to będzie po prostu:

	π		π		π		π
| f(ξ1) *		+ f(ξ1) *		− f(ξ1) *		− f(ξ1) *		| = |−1| = 1,
	4		4		4		4

czy:

	π		π		π		π
| f(ξ1) *		| + |f(ξ1) *		| + |f(ξ1) *		| + | f(ξ1) *		| = 1 +
	4		4		4		4

	π√2
		?
	4

Nienor: A racja, pisze 4

asdf:

	π
czyli suma całkowa to −		tak ?
	4

Trivial: Tak.

asdf: dzieki, o to mi chodziło

asdf: Mam teraz takie zadanie: Dany jest punkt A(−1,2,0) oraz prosta l: x= t, y = −1 + 2t, z = −1 − 3t Sprawdzic czy punkt lezy na prsotej, wystarczy: x = t y = −1 + 2t z = −1 − 3t podstawiając: −1 = t ⇒ t = −1 2 = −1 + 2t ⇒ 2t = 3

	1
0 = −1 − 3t⇒ t =
	3

czyli sprzeczność, tak ?

asdf: dalej mam : jesli nie, to znaleźć rzut punktu A na prostą l: x = t y = −1 + 2t z = −1 − 3t n^→ = [1, 2, −3] wektor AP₀^→ = [t +1, −1 + 2t − 2, −1 − 3t] = [t+1, 2t − 3, −3t − 1] rzut czyli musi byc prostopadły więc: AP₀^→ * n^→ = 0 [t+1, 2t − 3, −3t − 1] * [1,2,−3] = 0 t+1 + 4t − 6 + 9t + 3 = 0 14t − 2 = 0

	1
t =
	7

	1		2		3
P0 = (		, −1 +		, −1 −		) tak?
	7		7		7

Trivial: Z pierwszego równania wyliczasz t. x = t → t = −1. Potem tylko podstawiasz... y = −1 − 2 = −3 sprzeczność.

Trivial: Wygląda OK.

asdf: ok, dzieki

Trivial: Inna metoda: Macierz rzutu prostokątnego P na wektor n = [1 2 −3]^T jest macierz

	nnT		1
P =		=		[1 2 −3]T[1 2 −3]
	nTn		14

Rzut punktu A na prostą L to:

	1
A' = P0 + P(A − P0) = [0 −1 −1]T +		[1 2 −3]T[1 2 −3][−1 3 1]T
	14

	1
= [0 −1 −1]T +		[1 2 −3]T*(−1 + 6 − 3)
	14

	1		1
=		[0 −7 −7]T +		[1 2 −3]T
	7		7

	1
=		[1 −5 −10]T
	7

Trivial: gdzie P₀ oznacza punkt należący do prostej (P₀ = [0 −1 −1]^T)

asdf: skąd ty to wszystko umiesz...?

Trivial: Miałem podstawy algebry liniowej.

asdf: podstawy....