proszę o pomoc patryk: witam, proszę o pomoc w rozwiązaniu tych zadań. z góry dziękuję 1) ∫(x²+3√x²+sinx+4ex) dx = 2) ∫ x/√2x²+3 dx = 3) ∫ xdx/√x+1= 4) oblicz pole figury ograniczonej krzywymi: y=x2−1 ; y=x+1 5) Oblicz objętość bryły powstałej z obrotu dookoła osi OX. y=x3 ; 1≤x≤2 6) 3+2i/2+i + 1−i/1+2i + (3−i)2 = 7) (−1−√3i)8 = 8) x2/y x dy/dx=x3+1 9) dy/dx +3y=7e4x 10) dy/dx + y = 4sin2x 11) y"+4y'+4y=x2+3 12) y"+2y'+5y=0

patryk: kwadratu nie zaznaczyłem w kilku zadaniach. poprawione: 4) oblicz pole figury ograniczonej krzywymi: y=x²−1 ; y=x+1 5) Oblicz objętość bryły powstałej z obrotu dookoła osi OX. y=x³ ; 1≤x≤2 6) 3+2i/2+i + 1−i/1+2i + (3−i)² = 7) (−1−√3i)⁸ = 8) x²/y x dy/dx=x³+1 9) dy/dx +3y=7e⁴x

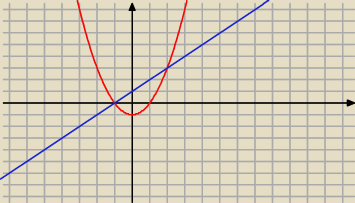
Patryk: 4) ∫(x+1−[x²−1])dx od −1 do 2

Patryk: 2) 3) podstawienie

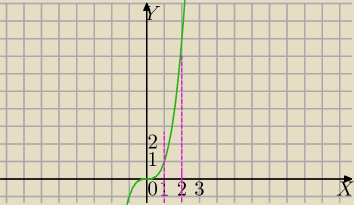
Mila: 5) Oblicz objętość bryły powstałej z obrotu dookoła osi OX. y=x³ ; 1≤x≤2 Rysunek

	1
V=π1∫2y2dx=π1∫2x6dx=π*[		x7]12=
	7

	1		127π
=π*		*(27−17)=
	7		7

Mila:

	3+2i		1−i
6)		+		+ (3−i)2 =
	2+i		1+2i

	3+2i		2−i		1−i		1−2i
=		*		+		*		+9−6i+i2=
	2+i		2−i		1+2i		1−2i

	6−3i+4i−2i2		1−2i−i+2i2
=		+		+8−6i=
	4−i2		1−4i2

	6+i+2		1−3i−2		8+i−1−3i		40		30i		1
=		+		+8−6i==		+		−		=		(47−32i)
	5		5		5		5		5		5

Mila: 7) (−1−sqrt(3)i)⁸ = W postaci algebraicznej [(−1−√3 i)²]⁴=(1+2√3i+3*i²)⁴=[(2√3i−2)²]²= =(4*3i²−8√3i+4})²=(−8−8√3i)²=64+128√3i+64*3i²= =64+128√3i−192=−128+128√3i w postaci trygonometrycznej z=−1−√3 i |Z|=2

	1		√3		π		4π
cosα=−		i sinα=−		⇔α=π+		=
	2		2		3		3

	4π		4π
z=2*(cos		+sin		i)
	3		3

	4*8π		4π*8
z8=28*((cos		+sin		i)
	3		3

	2π		2π
z8=256*((cos		+sin		i)
	3		3

	1		√3
z8=256*(−		+		)=−128+128√3i
	2		2

patryk: witam, a to 4 zadanie może dokładniej rozpisać? ja mam 2 sposobami i nie wiem, który jest prawidłowy. przy całce jakby co wszędzie u góry 2, a na dole −1

	x3		23
1) S=∫(x+1)dx − ∫(x2−1)dx= ∫(x+1+x2−1)dx= ∫(x2+x)dx=		+ x2=		+
	3		3

	8
22=		+4= 8/4+13/3=20/3=6 2/3
	3

	x3
2) S=∫(x+1)dx − ∫(x2−1)dx= ∫xdx + ∫dx − ∫ x2 dx = ∫dx= x2| = x| −		| − x|= 22
	3

	23		(−1)3
−(−1)2+2−1−(		+		) − (2−1) = 4−1+1−3=5−4=1
	3		3

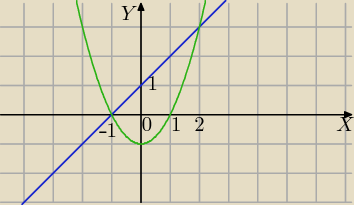
Mila: Zadanie 4) granice całkowania : x+1=x²−1 x²−x−2=0 Δ=1+8=9

	1−3
x1=		=−1 lub x2=2
	2

	−1		1
P=−1∫2(x+1−(x2−1))dx=−1∫2(−x2+x+2)dx=[		x3+		x2+2x]−12=
	3		2

	−1		1		−1		1
=		*23+		*22+2*2−(		*(−1)3+		*(−1)2+2*(−1))=
	3		2		3		2

	1
=4
	2

patryk: to należy do obu tych liczb podstawiać? patrząc w notatki z wykładów, podstawialiśmy tylko tą wyższą liczbę

Mila: Bo może po podstawieniu drugiej zerowało się.

patryk: a nie jest wynik = 1 1/2 ? już któraś godzina przy tej matmie i bania boli ^^

Mila: Wynik jest 4,5.

−8		1		1
	+2+4−(		+		−2)=
3		3		2

	2		2		3		1		1		2		1		3
6−2		−(		+		−2)=3		−(−1		)=3		+1		=4		=4,5
	3		6		6		3		6		6		6		6

patryk: no tak. dziękuję. pominąłem ten nawias. czas trochę odpocząć już chyba

Mila: