całka trygonometryczna matroz: Witam, mam problem z policzeniem

	xsinx
∫
	1+cos2x

Jaki sposób wykorzystać? Próbowałem już wszystkiego i nie dałem rady.

Nienor: http://www.wolframalpha.com/input/?i=%5Cint+%28%5Cfrac%7Bxsinx%7D%7B1%2B%28cosx%29%5E2%7D%29dx hmm... nie dziwię się.

matroz: widziałem to ale mam zadanie żeby z tego policzyc oznaczoną od 0 do pi...

Nienor: A miałeś całki podwójne

wredulus_pospolitus:

	x*sinx		sinx
∫		dx = ∫x*		dx
	1+cos2x		1+cos2x

	sinx
u' =		; v= x
	1+cos2x

u = −arctg(cosx) ; v' = 1

	sinx
∫x*		dx = xarctg(cosx) +∫arctg(cosx) dx
	1+cos2x

i tyle zrobisz ... nic więcej nie zrobisz

wredulus_pospolitus: ewentualnie można pokombinować i zauważyć, że arctg(cosx) jest to funkcja odwrotna do tg(cosx) tg(cosx) jest to funkcja symetryczna względem punktu A(π/2 ; 0) (czyli jest 'nieparzysta' względem x=π/2) ... więc całka z niej =0 skoro ∫tg(cosx) dx = 0 to także całka z funkcji odwrotnej będzie =0 czyli masz do obliczenia

	π		π2
(xarc(cosx))0π = πarctg(cosπ) − 0*..... = π*(arctg(−1)) = π*(−		) = −
	4		4

wredulus_pospolitus: oczywiscie pod hasłem 'więc całka z niej' oznacza ... 'więc całka w granicach 0 <−> π'

wredulus_pospolitus: i jakiegoś byka walnąłem ... bo powinna wyjść wartość na +

wredulus_pospolitus: ach ... już widzę ... powinno być −x*arctg(cosx)

matroz: @Wredulus zrobilem tyle co w Twoim 1−szym poście " funkcja symetryczna względem punktu A(π/2 ; 0) (czyli jest 'nieparzysta' względem x=π/2) ... więc całka z niej =0" tego nie rozumiem za bardzo, skąd ten pomysł, co to za własność? Odpowiedź prawidłowa, dziękuję za pomoc, prosiłbym jeszcze o wyjaśnienie

wredulus_pospolitus: tgx <−−− funkcja nieparzysta (symetria względem (0,0) ) cosx <−−− funkcja 'nieparzysta względem x=π/2' (zapraszam do wykresu cosinusa) cosx ∊<−1;1> tgx na odcinku <−1;1> jest nieparzystą funkcją z nieparzystości funkcji cosx wiemy, że ∀_{x1∊<0;π/2>} ∃_{x2∊<π/2;π>} cos(x₁) = −cos(x₂) = k ; gdzie k∊<0;1> z nieparzystości funkcji tgx wiemy, że ∀_x1∊<0;1> ∃_{x2∊<−1;0>} tg(x₁) = −tg(x₂) ze złożenia zatem mamy: ∀_{x1∊<0;π/2>} ∃_{x2∊<π/2;π>} tg(cos(x₁)) = −tg(cos(x₂))

matroz: Okej to wszystko wiem Tylko nie rozumiem skąd wniosek : "więc całka z niej =0"

Trivial:

matroz: aa teraz chyba rozumiem chodzi o to że dla ∫arctg(cosx)dx F(pi) − F(0) = 0 ?

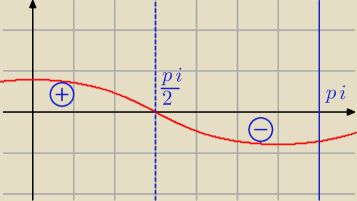
Trivial: Chodzi o to, że dla funkcji arctg(cosx) korzystając z interpretacji geometrycznej całki stwierdzamy że jest ona równa 0. Funkcja arctg(cosx) w przedziale [0,π] ma dokładnie taką samą część pola pod wykresem i nad wykresem.

matroz: Ok, dzięki wielkie za pomoc i wyjaśnienia!