Obliczyć pole obszaru ograniczonego funkcjami
Karol: Obliczyć pole obszaru ograniczonego funkcjami: y=−x2+4 i y=x2−4x+4
20 cze 23:32
Vizer:
Narysuj sobie te krzywe i wyznacz punkty przecięcia się będące granicami całkowania.
20 cze 23:47
Mila:
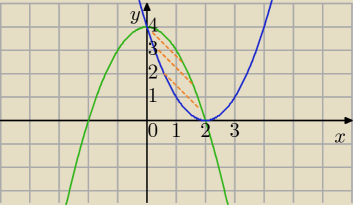
rysunek
y=−x2+4
y=x2−4x+4
Punkty przecięcia wykresów
x
2−4x+4=−x
2+4
2x
2−4x=0
x(2x−4)=0
x=0 lub x=2 granice całkowania
| | −2 | |
P=0∫2(−x2+4−(x2−4x+4))dx=0∫2(−2x2+4x)=[ |
| x3+2x2]02= |
| | 3 | |
| | −2 | | −8 | | 16 | |
= |
| *23+2*22−0= |
| +8= |
| |
| | 3 | | 3 | | 3 | |
20 cze 23:56