
 f'(x)=0⇔−2x*e−x2=0⇔x=0
f'(x)>0⇔funkcja f(x) jest rosnąca
−2x*e−x2>0⇔−2x>0⇔x<0
f'(x)<0⇔ f(x) jest malejąca
−2x*e−x2<0⇔x>0
dla x=0 funkcja ma ekstremum, pochodna zeruje sie i zmienia znak przy przejściu przez punkt
(0,0)
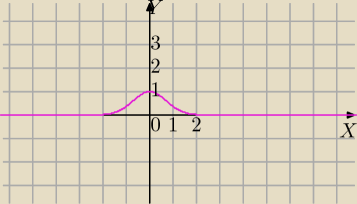
Dla x=0 funkcja ma maksimum ymax=e0=1
f'(x)=0⇔−2x*e−x2=0⇔x=0
f'(x)>0⇔funkcja f(x) jest rosnąca
−2x*e−x2>0⇔−2x>0⇔x<0
f'(x)<0⇔ f(x) jest malejąca
−2x*e−x2<0⇔x>0
dla x=0 funkcja ma ekstremum, pochodna zeruje sie i zmienia znak przy przejściu przez punkt
(0,0)
Dla x=0 funkcja ma maksimum ymax=e0=1
| 1 | ||
lImx→∞e−x2=limx→∞( | )x2}=0 | |
| e |
| 1 | ||
lImx→−∞e−x2=limx→∞( | )x2}=0 | |
| e |

