Obraz punktu względem prostej Eis22: Znajdź obraz punktu A(3,−1) w symetrii względem prostej −3x+2y=1 Rozwiązuję to już od 30 min i cały czas wychodzą mi jakieś dziwne wyniki. Robię to w następujący sposób.

	2
1. Szukam prostej prostopadłej, wychodzi mi to: y=−		x+1
	3

	3		11
2. Z tych obu prostych rozwiązuję układ równań i wychodzi mi: D(				), jest to
	13		13

punkt, w którym proste się przecinają.

	xa+xa'		ya+ya'
3.stosuję wzory: xd=		yd=
	2		2

	−33		35
Wynik: A'(		,		)
	13		13

Wydaje mi się, że wynik jest zły. Czy ktoś to może potwierdzić?

Eis22: Halo : d?

b.: ja nie widzę żadnego błędu

Eta: ok

Eis22: Ej, to super. Dziękuję za rozwianie moich wątpliwości : )

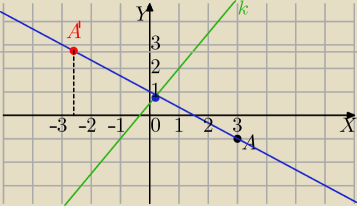
Mila: Znajdź obraz punktu A(3,−1) w symetrii względem prostej −3x+2y=1 rysunek 2y=3x+1

	3		1
k: y=		x+
	2		2

Punkt A" symetryczny do A względem prostej K leży na prostopadłej do k i przechodzącej przez punkt A

	2		−2
p: y=−		x+b i −1=		*3+b⇔b=1
	3		3

	−2
p: y=		x+1
	3

Punkt przecięcia prostych:

−2		3		1
	x+1=		x+
3		2		2

	3		11
x=		, y=
	13		13

A'=(x,y}

3		x+3		7
	=		⇔x=−2
13		2		13

11		y−1		9
	=		⇔y=2
13		2		13

Wszystko zgadza się.