Błagam pomóżcie Wojtek: Proszę o pomoc. Oblicz boki trójkąta ABC, gdy |BC| = 10, β=30 stopni, γ= 45 stopni. Oczywiście nei ejst to trójkąt prostokątny.

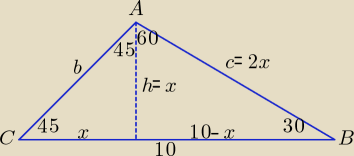
Bogdan: Ten rysunek powinien pomóc. Można też zastosować twierdzenie sinusów.

Wojtek: Zastosowałam to twierdzenie i mam wyniki, tyle, że trochę dziwne. Czy mógłbys mi sprawdzić, zcy sa dobre?

Wojtek: b = 5√6 − 5√2 c = 10√3 − 10 ?

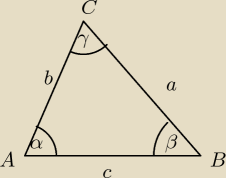
nalepek: a=10 β=30^o γ=45^o korzystaj z twierdzenia sinusów

a		b
	=
sinα		sinβ

10		b
	=
sin105o		sin30o

	√3		√2
sin105o=sin(45o+60o)=sin60o*cos45o+sin45o*cos60o=		*
	2		2

	√2		1		√6+√2
+		*		=
	2		2		4

10		b
	=
√6+√2   4		12

	√6+√2
10*12=		b /*4
	4

20=(√6+√2)b / : (√6+√2)

20
	=b
√6+√2

20		√6−√2
	*		=b
√6+√2		√6−√2

	20(√6−√2)
b=
	4

b=5(√6−√2)

nalepek: hah, nie pomyslalem ^^ taa. wyniki bedziesz mial dobre (pkt C juz nie robie, bo masz i tak prosciej opisane )

Bogdan: Wyniki są dobre.

nalepek:

c		b
	=
sin45o		sin30o

c		5√6−5√2
	=
√22		12

c
	=(5√6−5√2)*√22 /*2
2

c=(5√6−5√2)*√2 c=5√12−10 to chyba nie miales dobrze (chyba ze ja sie pomylilem ;x)

nalepek: błe. c=10√3−10

Wojtek: Dziękuje