oblicz pole (całki ) adam: y=2x²,y=x oraz y=x² ,x∊(2,4) jestem w dziale całki oznaczone nie mam pojęcia jak się za to zabrać to pierwsze to mam obliczyć P a drugie V

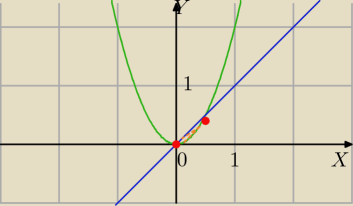
Mila: Rysunek: 1) y=2x² y=x Punkty przecięci wykresów 2x²=x 2x²−x=0

	1
x=0 , x=		granice całkowania
	2

	1		2
P=0∫{(1/2)}(x−2x2) dx= [		x2−		x3]012=
	2		3

	1		1		2		1
=		*(		)2−		*(		)3−0=
	2		2		3		2

	1
=
	24

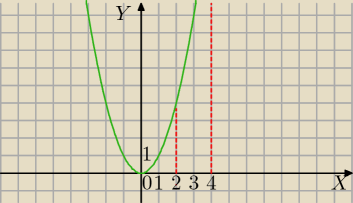Mila: 2) y=x² x∊<2,4> obrót wokół OX

	1
V=π2∫4y2 dx=π2∫4(x2)2dx=π2∫4x4 dx=π*		[x5]24=
	5

	1
=π		*(45−25)=dokończ
	5