sup inf pepe: wyznaczyć inf, sup, lim inf, lim sup z następującego ciągu:

	3n + 2		2
(−1)n * (		) + (−1)n * (3 +		)
	n		n

wredulus_pospolitus: znasz definicje tych pojęć jeżeli tak to w czym właściwie tkwi problem

PW: Pytanie pomocnicze: Dobrze przepisałeś, czy Uczelnia sprawdza Twoją inteligencję − czy widzisz, że

	3n+2		2
		= 3+		.
	n		n

pepe: Znam definicję supremum i infimum i tu wychodzi mi inf = −10, sup = 8. Ale nikt nie potrafi mi wytłumaczyć czym jest lim sup i lim inf. Mógłby ktoś? PW: tak, odnotowałem to.

wredulus_pospolitus: http://pl.wikipedia.org/wiki/Granice_dolna_i_g%C3%B3rna teoria odnośnie lim sup i lim inf

pepe: Gdybym rozumiał tę definicje, to nie pytałbym na forum. Potrzebuję, żeby ktoś mi wytłumaczył jak krowie na rowie . Btw. czy ktoś może potwierdzić lub obalić moją teorię na temat infimum i supremum?

wredulus_pospolitus: a jaka jest 'Twoja teoria' na temat inf i sup lim inf jest to to nic innego jak granica z inf lim sup jest to granica z sup jeżeli ciąg jest zbieżny to lim inf a_n=lim sup a_n = lim a_n

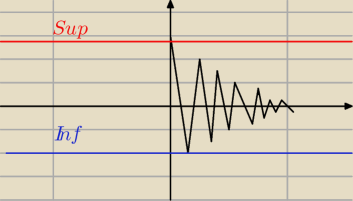
pepe: Dobra... Spróbujmy w ten sposób: przez Ograniczenie górne rozumiem każdą liczbę M taką, że dowolny wyraz ciągu jest mniejszy lub równy od M. Kres górny to najmniejsza możliwa liczba M, tzn największy wyraz ciągu, albo wartość do której ciąg zbiega, ale nigdy jej nie osiąga. z dołem jest analogicznie. Czyli rysuję sobie osie x i y, zaznaczam na wykresie kolejne wyrazy ciągu i stawiam poziomom kreskę tak, żeby pokrywała się z "najwyższym" punktem, albo z wartością do której zbiega ciąg. Tak czy inaczej, powyżej tej linii nie ma już żadnego punktu na układzie. Dobrze myślę, czy źle?

wredulus_pospolitus: dobrze myślisz ... jedna (ważna) uwaga Sup to NAJMNIEJSZA taka liczba M, że dowolny wyraz ciągu będzie nie większy od tej liczby Inf to NAJWIĘKSZA taka liczba m, że dowolny wyraz ciągu będzie nie mniejszy od tej liczby bez tego to sup a_n = na przykład 10^{2345628872687492}

wredulus_pospolitus: natomiast lim sup i lim inf to są 'graniczne' suprema i infinia tegoż ciągu

pepe: Nie bardzo rozumiem, co znaczy "graniczne" suprema i infima. żeby dostać lim inf mam policzyć granicę tegoż ciągu przy n dążącym do inf?

pepe: ktos wie?

pepe: no litości... jutro mam poprawkę, niechże ktoś wytłumaczy

b.: 1. bierzemy inf_k>n a_k, czyli infimum wyrazów tego ciągu, ale od wyrazu n+1 począwszy 2. dostajemy w ten sposób nowy ciąg zależny od n 3. liczymy jego granicę, lub jego supremum, co na jedno wychodzi, bo jest to ciąg rosnący (słabo) otrzymana wartość to liminf a_n inna, równoważna definicja jest taka: liminf a_n to infimum zbioru punktów skupienia ciągu (a_n). x ∊ Ru{−∞, ∞} jest punktem skupienia (a_n), jesli z (a_n) można wybrać podciąg zbieżny do x