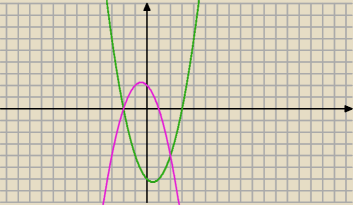
Oblicz pole obszaru ograniczonego parabolami : Milka: Oblicz pole obszaru ograniczonego parabolami : y=x² − x − 6 y= −x² − x + 2 Na początku co muszę zrobic? Do jednego i drugiego policzyć deltę?

bez: ∫₁²(x²−x−6−(−x²−x+2))dx

Milka: dziękuje o to mi chodziło

bezendu: Milka ale ja nie wiem czy to jest dobrze ale chyba tak

Milka: Zaraz rozważę to sprawdzę jeszcze z odpowiedzią Bo zagubiłam się już na samym początku

bezendu:

Vizer: No chyba coś nie tak, po pierwsze granice całkowania są −2 ≤ x 2, bo dla x = −2 i x = 2 te wykresy się przecinają, po drugie "wyższą" funkcją na tym przedziale jest y = −x² − x + 2, a "niższą" y = x² − x − 6, więc pole powierzchni możemy zapisać tak: |D| = ∫₋₂² (−x² − x + 2 − (x² − x − 6)) dx = ...

Mila: y=x² − x − 6 y= −x² − x + 2 Ustalamy granice całkowania: x² − x − 6= −x² − x + 2 2x²=8 x²=4 x=−2 lub x=2 P=₋₂∫²(−x² − x + 2 −(x²−x−6))dx=

	−2
=−2∫2(−2x2+8)dx=[		x3+8x]−22= obliczaj
	3

	1
=21
	3

Vizer: Edukacyjnie : http://www.wolframalpha.com/input/?i=area+between+y%3Dx^2-x-6+and+y%3D-x^2-x%2B2