 na rysunki przedstawiono wykres funkcji kwadratowej f(x)= ax2+bx+c gdzie a≠0
na rysunki przedstawiono wykres funkcji kwadratowej f(x)= ax2+bx+c gdzie a≠0
| f(7) | ||
oblicz wartość wyrażenia | ||
| f(−2) |
| f(7) | 49a+7a−42a | 14a | |||
= | = | = − 72
| |||
| f(−2) | 4a−2a−6a | −4a |
| 25 | −Δ | ||
= | |||
| 16 | 4a |
| −3 + 2 | 1 | 25 | ||||
W = (xw, yw), xw = | = − | , yw = | ||||
| 2 | 2 | 16 |
| 25 | 1 | 1 | 25 | 25 | 1 | ||||||
= a*(− | + 3)*(− | − 2) ⇒ | = − | ⇒ a = − | |||||||
| 16 | 2 | 2 | 16 | 4 | 4 |
| 1 | 1 | |||
f(x) = − | (x + 3)(x − 2) ⇒ f(x) = − | (x2 + x − 6) ⇒ | ||
| 4 | 4 |
| 1 | 1 | 3 | ||||
⇒ f(x) = − | x2 − | x + | ||||
| 4 | 4 | 2 |
| f(7) |
| 50 | 25 | |||||||||||||
= | = | = − | ||||||||||||||
| f(−2) |
| −4 | 2 |
 .
xw oraz yw to współrzędne wierzchołka paraboli.
.
xw oraz yw to współrzędne wierzchołka paraboli.
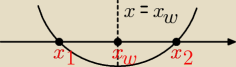 Myślę, że rysunek odpowiada na pytanie anonima. Prosta x = xw jest osią symetrii
paraboli.
Myślę, że rysunek odpowiada na pytanie anonima. Prosta x = xw jest osią symetrii
paraboli.
| 25 | ||
może ktoś pokazać jak doszedł Bogdan do tych | ||
| 16 |
| 25 | ||
Wartość | jest podana w treści zadania, cytuję: "największa wartość funkcji | |
| 16 |