objętość bryły hp: Objętość bryły powstałej z obrotu dookoła osi x−ów obszaru ograniczonymi liniami: y = x² y = x Wiem +/− jak wygląda ta bryła, bo sobie rozrysowałem. Znam też wzór, ale nie umiem go zastosować jak są dwie funkcje podane.

hp: V = π∫_a^b f(x)² dx jeżeli jest jedna funkcja to jest ok, bo obliczam sobie, całkuję, podstawiam i jest ok, ale z dwoma nie wiem jak zrobić.

Vizer: A jakbyś odjął objętość powstałą przez obrót y = x od objętości powstałej przez obrót y = x² (oczywiście dla odpowiednich granic całkowania), to co by Ci wyszło? ;>

hp: narysowałem b=0, a = 2 , bo w takim przedziale na osi x mieści się ten obszar.

	x3		1*x2		8		4		16		12
V=π∫02 x2 − x dx = ∫02		−		=		−		=		−		=
	3		2		3		2		6		6

	4
		π
	6

za łatwo się to zrobiło. więc pewnie tak nie będzie, proszę o sprawdzenie.

Vizer: A obszar nie jest 0 ≤ x ≤ 1 ?

123: Wzór, któy musisz zastosować to: |V| = π∫_a^b[g²(x) − f²(x)]dx, gdzie g²(x) ≥ f²(x)

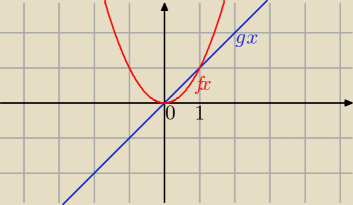
123: Czyli w twoim przypadku: |V| = ∫₀¹[x − x²]dx

hp: |V| = π∫ab[g2(x) − f2(x)]dx, gdzie g2(x) ≥ f2(x) no okey, czyli tak jak robiłem jedna funkcja − druga funkcja, tylko skąd mam wiedzieć w jakiej kolejności, która jest większa?

	1
Wynik po podstawieniu wyszedł mi		π
	6

hp: mam kolejną bryłę y=5x − x² czyli y=−x² + 5x , y≥0, jak tutaj określić te punkty a i b ? proszę o sprawdzenie poprzedniego