| |z−3| | ||
dane równanie: | ≥ 1 | |
| |2i−z| |
| |z−3| | |
≥ 1 /*|2i−z| | |
| |2i−z| |
| 1 | 5 | |||
−1 | + | ≥ y | ||
| 2 | 4 |
 )
z*z = 1+(2−i)*z+(2+1)*z
(x+iy)*(x−iy) = 1+(2−i)*(x+iy)+(2+i)*(x−iy)
x2−i2−y2 = 1+2x+2iy−xi+y+2x−2iy+xi+y
x2+y2 = 1+4x+2y
(x2−4x+2)+(y2−2y+1) = 1+2+1
(x−2)2+(y−1)2=4
zatem wychodzi mi: S(2,1) r=2
ale niestety wynik podany w odpowiedziach to: Okrąg o środku 2+i, czyli S(2,1) i promieniu 62
)
z*z = 1+(2−i)*z+(2+1)*z
(x+iy)*(x−iy) = 1+(2−i)*(x+iy)+(2+i)*(x−iy)
x2−i2−y2 = 1+2x+2iy−xi+y+2x−2iy+xi+y
x2+y2 = 1+4x+2y
(x2−4x+2)+(y2−2y+1) = 1+2+1
(x−2)2+(y−1)2=4
zatem wychodzi mi: S(2,1) r=2
ale niestety wynik podany w odpowiedziach to: Okrąg o środku 2+i, czyli S(2,1) i promieniu 62

 1)
|z−3|≥|2i−z|
z=x+iy
|x+iy−3|≥|2i−x−iy|
|(x−3)+iy|≥|(−x)+(2−y)i|
(x−3)2+y2≥x2+(2−y)2 stąd
1)
|z−3|≥|2i−z|
z=x+iy
|x+iy−3|≥|2i−x−iy|
|(x−3)+iy|≥|(−x)+(2−y)i|
(x−3)2+y2≥x2+(2−y)2 stąd
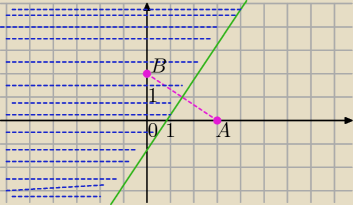
| 3 | 5 | |||
y≥ | x− | równanie symetralnej AB, | ||
| 2 | 4 |
| 3 | 5 | |||
y= | x− | i geometryczna interpretacja w układzie wsp. | ||
| 2 | 4 |

 W pierwszym , punkt B∉do zbioru rozwiązań, mianownik ma byc ≠0.
Zadanie2)
(x+iy)(x−iy)=1+(2−i)(x+iy)+(2+i)(x−iy)
x2+y2=1+2x+2iy−ix−i2y+2x−2iy+ix−i2y
x2+y2=1+2x+y+2x+y
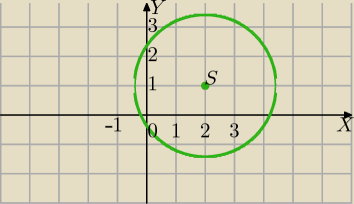
x2+y2−4x−2y=1
(x−2)2−4+(y−1)2−1=1
(x−2)2+(y−1)2=6⇔
(x−2)2+(y−1)2=(√6)2
S=(2,1) r=√6
W pierwszym , punkt B∉do zbioru rozwiązań, mianownik ma byc ≠0.
Zadanie2)
(x+iy)(x−iy)=1+(2−i)(x+iy)+(2+i)(x−iy)
x2+y2=1+2x+2iy−ix−i2y+2x−2iy+ix−i2y
x2+y2=1+2x+y+2x+y
x2+y2−4x−2y=1
(x−2)2−4+(y−1)2−1=1
(x−2)2+(y−1)2=6⇔
(x−2)2+(y−1)2=(√6)2
S=(2,1) r=√6

