przedziały wklęsłości i wypukłości oraz punkt przegięcia funkcji hp: przedziały wklęsłości i wypukłości oraz punkt przegięcia funkcji Nie wiem jak to się wyznacza, ale przeczytałem, że należy zacząć od pierwszej i drugiej pochodnej.

	x2
f(x) =
	x−1

	2x *(x−1) − x2 * 1		x2 − 2x
f'(x) =		=
	(x−1)2		(x−1)2

	(2x−2) * (x − 1)2 − (x2−2x) * 2(x−1) * 1
f''(x) =
	(x−1)4

	(2x−2) * (x2 − 2x +1) − (x2−2x) * 2(x−1) * 1
f''(x) =
	(x−1)4

f''(x) = U{(2x³ − 4x² + 2x − 2x² + 4x −2) − ( 2x³ − 2x² − 4x² + 4x)}{(x−1)⁴ f''(x) = U{2x³ − 4x² + 2x − 2x² + 4x −2 − 2x³ + 2x² + 4x² − 4x}{(x−1)⁴ po redukcji zostało

	2x−2		2(x−1)
f''(x) =		=		4
	(x−1)4		(x−1

teraz co dalej się robi.

aniabb: punkt przegięcia jak f'' =0 tutaj brak wypukła jak f'' >0 tutaj x>1 wklęsła jak f''<0 tutaj x<1

hp: muszę zacząć od początku, bo coś źle wyliczyłem + poczytałem i jest napisane żeby nie wymnażać tego wszystkiego tyle wyciągnąć część wspólną przed nawias.

hp: muszę zacząć od początku, bo coś źle wyliczyłem + poczytałem i jest napisane żeby nie wymnażać tego wszystkiego tyle wyciągnąć część wspólną przed nawias.

hp: aniabb czyli, czyli co najlepiej wyciągnąć przed nawias w 3 linijce? Bo coś nie widzę tego.

hp: może tak ?

(2x−2) * (x−1)2 − (x2 − 2x) * 2(x−1)		2(x−1)[(x−1) − (x2 − 2x)]
	=		=
(x−1)4		(x−1)4

	2(x−1)(x−1−x2+2x)
	(x−14

aniabb: obojętnie..ale poprzednio dobrze miałeś

hp: ale tutaj raczej będę miał błąd, bo jeżeli wyciągnełem sobie z 2(x−1) to nie mogę opuścić jednej potęgi z (x−1)².

(2x−2) * (x−1)2 − (x2 − 2x) * 2(x−1)		2(x−1)[(x−1)2 − (x2 − 2x)
	=		4 =
(x−1)4		(x−1)

	2(x−1)(x2 −2x + 1 − x2 + 2x)
		tylko, że po daje to taki wynik, więc chyba tak być
	(x−1)4

	2(x−1) *1
nie może
	(x−1)4

hp: kurczę, czyli wyciągając przed nawias i/lub mnożąc doszedłem do takiej samej postaci, to dobrze, o ile to zrobiłem dobrze. Jeżeli to jest dobrze, to jakie kroki przyjąć następnie? Wiem, że teraz trzeba to pomnożyć * (x−1)⁴ żeby się pozbyć mianownika. Więc zostanie tylko 2(x−1)

aniabb: przecież się skraca w nawiasie i wychodzi tak jak było

aniabb: no i sprawdzasz kiedy t jest >=<od zera pamiętając że x=1 nie nalezy do dziedziny

hp: czyli mogę to robić mnożąc wszystko razy wszystko i wyciągając część wspólną przed nawias czyli x=1 czyli w punktu przegięcia nie ma tak? Bo jeżeli by należała do dziedziny to punkt by istniał. ale jak narysować przybliżony wykres? funkcja będzie wypukła?

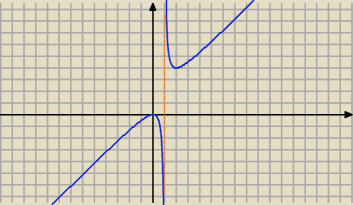
aniabb: wypukła dla x>1 wklęsła dla x<1 patrzymy na nią od dołu bo w kierunku osi Y

aniabb: pisałam odpowiedź o 15:58

hp: a przedziały wklęsłości i wypukłości?

hp: a przedziały wklęsłości i wypukłości?

aniabb: ile razy mam pisać wypukła dla x > 1 to jest przedział ..... inaczej x∊(1;∞) skoro ten czerwony jest dla Ciebie nieczytelny

hp: okey, dziękuje bardzo za pomoc