geometria w przestrzeni niedouczonaMatematyczka: Kulę o objętości 288 π cm² przecięto odległą od środka kuli o 3 cm. Oblicz pole przekroju kuli. NAPRAWDĘ PROSZĘ O ROZWIĄZANIE !

Janek191:

	4		3
V =		π R3 = 288 π / *
	3		4

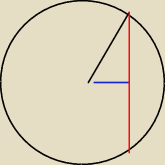
π*R³ = 216π / : π R³ = 216 R = ³√216 = 6 −−−−−−−−−−−−−− Przekrojem kuli jest koło o promieniu długości r d = 3 cm Z tw. Pitagorasa mamy d² + r² = R² r² = R² − d² = 6² − 3² = 36 − 9 = 27 = 9*3 r = √9*3 = 3 √3 −−−−−−−−−−−−− Pole przekroju ( koła) : P_p = π *r² = π* [ 3 √3)² = π *9*3 = 27 π Odp. P_p = 27 π cm² =================== Rysunek: R = 6 − czarny kolor d = 3 − niebieski kolor r − połowa cięciwy − czerwony kolor

aniabb: https://matematykaszkolna.pl/forum/207275.html