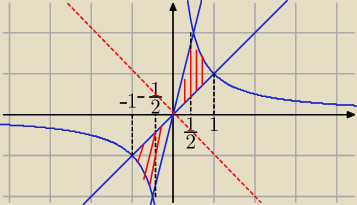
. lina: znowu calki potrójne...musze okreslic obszar dla krzywych z=x+y, z=0,xy=1,y=x,y=4x

Vizer: D₁: D₂: D₃: D₄

	1		1		1		1
−1 ≤ x ≤ −		−		≤ x ≤ 0 0 ≤ x ≤				≤ x ≤ 1
	2		2		2		2

1		1
	≤ y ≤ x 4x ≤ y ≤ x x ≤ y ≤ 4x x ≤ y ≤
x		x

A jeśli masz policzyć np. objętość to wystarczy, że weźmiesz jeden z dwóch zestawów obszarów, albo D₁ i D₂, albo D₃ I D₄, bo płaszczyzna przechodzi w układzie OXY jako y = −x (czerwone zakreskowane), więc objętość będzie równa dla przedziałów −1 ≤ x ≤ 0 oraz 0≤ x ≤ 1, z tymże dla pierwszego płaszczyzna będzie pod OXY, dla drugiego nad OXY, co będzie skutkowało różnicą kolejności granic całkowania w całce trzeciej (po dz).

lina: aha.. kurcze skomplikowane troche..

Vizer: Nie aż tak, niestety nie da się zapisać tego obszaru za jednym zamachem, więc licząc objętość, powiedzmy że wybraliśmy zestaw dla przedziału 0 ≤ x ≤ 1, liczymy najpierw objętość dla obszaru

	1		1
0 ≤ x ≤		, następnie		≤ x ≤ 1, dodajemy te dwie objętości otrzymując już połowę
	2		2

całości, więc mnożąc jeszcze razy 2 otrzymujemy objętość po całym obszarze (−1 ≤ x ≤ 1)