geometria analityczna Diana: Podstawa trojkata rownoramiennego abc jest odcinek ab gdzie a(−2 1), b(6,1). wyznacz współrzędne wierzcholka c wiedzac ze nalezy on do prostej y=x+2. Czy moglby ktos wyjasnic to zadanie?

5-latek: ja bym zrobil to np tak ogolnie 1. Rysunek (cos podpowie ) 2 . Napisal rownanie symetralnej odcinka |AB| −dlaczego symetralna . czym jest jednoczesnie symetralna w trojkacie rownoramiennyn? . Z rysunku latwo je odczytac . Ale mozesz wyznaczyc . 3. Wyznaczyl punkt przeciecia sie symetralnej z prosta y=x+2 . Drugi sposob pewnie poda Mila ktora serdecznie pozdawiam . Milu na razie nie rysowalem bo mam inne powazniejsze sprawy na glowie

5-latek: bezendu teraz sprawdz czy dlugosc odcinka |AC|=|BC| musz byc rowne bo to jest trojkat rownaramienny. Jesli tak to jest OK

Mila: Witam 5−latku, równie serdecznie. Narysuję Twój sposób.

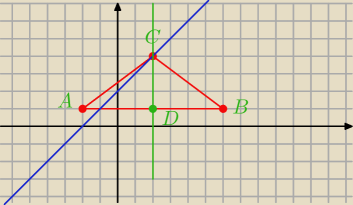
bezendu: D= środek AB D=(x;y) x=2 y=1 D=(2;1) prosta przechodząca przez punkty A i B 1=−2a+b 1=6a+b −2a+b=6a+b −2a−6a=0 a=0 1=b y=1 prostopadła do prostej AB; a=0 x=2 punkt przecięcia sie prostych x=2 i y=x+2 y=2+2=4 Niech moderatorzy usną mój pierwszy post w tym wątku

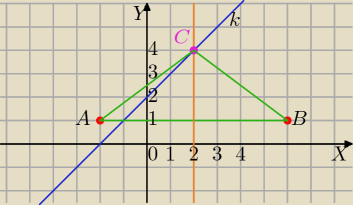
Mila: A(−2 ,1), B(6,1). k: y=x+2 1) ΔABC − Δ równoramienny Wysokość opuszczona z wierzchołka C jest symetralną AB s: s⊥AB i przechodzi przez środek AB

	−2+6
S=(		,1)=(2,1)
	2

s: x=2 symetralna AB ( tu jest to proste.) 2) C: y=2+2=4 C=(2,4)

5-latek: Milu mam na glowie teraz sprawe kominow w budunku . Bezendu ale sie wciales Mili . MIales wyznaczyc symetralna wektorami −przeciez wczoraj czy przedwczoraj liczyles . Ucz sie wektorow

bezendu: Zanim pisałem to nie było postu Mili a zauważyłem że źle rozwiązałem dlatego napisałem jeszcze raz z prośbą o usunięcie pierwszego postu Wektory powoli poznaje

pigor: ..., lub np. z warunków zadania a=(−2,1), b=(6,1}, c=(x,y)= (x,x+2)= ? , to |ac|= |bc| ⇔ ac²=bc² ⇔ (x+2)²+(x+2−1)² = (x−6)²+(x+2−1)² ⇔ ⇔ x²+4x+4 = x²−12x+36 ⇔ 16x= 32 ⇔ x=2 i y=x+2= 4 , zatem c=(2,4) − szukany wierzchołek Δabc. ...