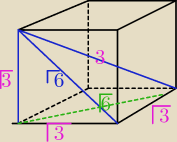
 skoro przekątna ściany bocznej =√6 więc krawędź a=√3 bo d=a√2
zatem przekątna sześcianu = 3
przekątna podstawy również √6
Pole powierzchni bocznej = √3•√3/2 +√6•√3/2+√3•√6/2 = 1,5+3√2
skoro przekątna ściany bocznej =√6 więc krawędź a=√3 bo d=a√2
zatem przekątna sześcianu = 3
przekątna podstawy również √6
Pole powierzchni bocznej = √3•√3/2 +√6•√3/2+√3•√6/2 = 1,5+3√2
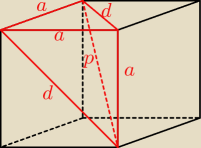 d=√6
d=a√2
p=a√3
a√2=√6
a=√3
Powierzchnia tego czworościanu to:
− 2 trójkąty prostokątne o bokach a, a, d
− 2 trójkąty prostokątne o bokach a, d, p
d=√6
d=a√2
p=a√3
a√2=√6
a=√3
Powierzchnia tego czworościanu to:
− 2 trójkąty prostokątne o bokach a, a, d
− 2 trójkąty prostokątne o bokach a, d, p
| 1 | 1 | |||
Pc=2* | a2+2* | ad=a2+a*a√2=a2(1+√2)=(√3)2(√2+1)=3(√2+1) | ||
| 2 | 2 |
| 1 | 3 | 6√2−3 | ||||
Pb=Pc− | a2=3√2+3− | = | ||||
| 2 | 2 | 2 |
 miało być bez podstawy
miało być bez podstawy 