okrag opisany na trojkacie Kuba: pomozcie prosze znalazlem tutaj podobne zadanie z trojkatem prostokatnym lecz w moim jest to trojkat dowolny zad. na trojkacie o wierzcholkach A=(−2,−3), B=(4,3), C=(0,3) opisano okrag o srodku S i promieniu R: − wyznacz wspolrzedne srodka S okregu opisanego na trojkacie ABC − oblicz jego promien R − napisz rownanie okregu opisanego na tym trojkacie ABC ( to chyba z jakiegos wzoru moge obliczyc podstawiajac wartosci prawda?)

JAPON1A: o: ( x − a )² + ( y − b)² = r² < −−− rownanie okregu ( jak wyliczysz a,b,r podstawiasz i masz odp. ) ( 2 + a )² + ( 3 + b)² = r² ( 4 − a)² + ( 3−b)² = r² a² + ( 3 − b )² = r² odejmujesz 2 rownanie od 3 16 − 8a + a² − a² = 0 => a = 2 podstawiasz a ,liczysz b i r R to odcinek od srodka okregu do jednego z wierzcholkow trojkata ( wzor na dlugosc odcinka ) r

Kuba: nie rozumiem skad wzaielas liczby do podstawienia za x i y i jak stworzylas te trzy rownania

5-latek: Moze Jakub narysuj na poczatek rysunek . Wiemy czym jest srodek okregu opisanego na trojkacie . Mozemy go rowniez wyznaczyc tak wyznacz rownanie symetralnej boku AB i np rownanie symetralnej boku BC. (albo bezwektorowo albo wektorami −twoja wola ) Wyznacz punkt przeciecia sie symetralnych i masz srodek okregu opisanego na trojkacie Promien R −juz podpowiedzial kolega i masz wszystko do zadania

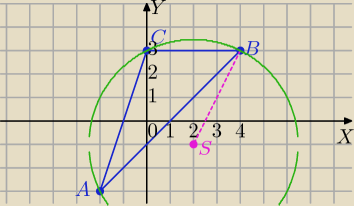
Mila: Na trojkącie o wierzcholkach A=(−2,−3), B=(4,3), C=(0,3) opisano okrag o srodku S . I sposób Równanie okręgu− postać kanoniczna. (x−a)²+(y−b)²=r² gdzie: r− promień, S=(a,b) współrzędne środka okręgu ( masz 3 niewiadome, a, b,r) Wsp. punktów :A,B,C spełniają to równanie: (−2−a)²+(−3−b)²=r² (4−a)²+(3−b)²=r² (0−a)²+(3−b)²⇔ 4+4a+a²+9+6b+b²=r² 16−8a+a²+9−6b+b²=r² a²+9−6b+b²=r² ⇔ 4+4a+a²+9+6b+b²=16−8a+a²+9−6b+b²⇔4+4a+9+6b=16−8a+9−6b a²+9−6b+b²=16−8a+a²+9−6b+b²⇔9−6b=16−8a+9−6b 12a+12b=12 8a=16⇔a=2 i b=−1⇔ 1) S=(2,−1), r=√2²+4²=√20=2√5 2) (x−2)²+(y+1)²=20 równanie okręgu II sposób współrzędne S znajdujesz jako punkt przecięcia symetralnych dwóch boków Jedna symetralna: x=2 Drugą napisz np. prostopadła do AB i przechodząca przez środek AB.