Zadanie Maturalne
bezendu:
Wyznacz x tak aby liczby x+4, x
2+4x, 10x+4 były kolejnymi wyrazami ciągu geometrycznego o
wyrazach całkowitych różnych od 0. (Czerwony aksjomat Test maturalny nr 2, zadanie 5)
(x
2+4x)
2=(x+4)(10x+4)
x
4+8x
3+16x
2=10x
2+4x+40x+16
x
4+8x
3+6x
2−44x−16=0
schemat Hornera
1 8 6 −44 −16
−4 1 4 −10 −4 0
W(x)=(x+4)(x
3+4x
2−10x−4)
1 4 −10 −4
2 1 6 2 0
W(x)=(x+4)(x−2)(x
2+6x+2)
Δ=6
2−4*1*2=28
√Δ=2
√7
i teraz tu nie wyjdą pierwiastki całkowite więc nie rozkładam
W(x)=(x−2)(x+4)(x
2+6x+2)
spr dla x=−4
−4+4=0 4
2−16=0 10*(−4)+4=−36 a
1=0 a
2=0 a
3=−36 nie jest ciągiem geometrycznym
spr dla x=2
6, 12 24 q=2=const więc jest geometryczny
Zgadza się zapis i obliczenia
16 cze 18:15
kulfon: wygląda na to że wszystko się zgadza. Nie masz odpowiedzi do tego ?
16 cze 18:20
bezendu: Nie mam tylko odbite testy do robienia w wakacje i dlatego napisałem z jakiego zbioru, może
ktoś ma i sprawdzi odpowiedź
16 cze 18:21
Karolina: Dla jakich wartości x liczby 1, 2sinx , cos2x są trzema kolejnymi wyrazami ciągu
geometrycznego?
16 cze 18:22
Karolina: Dla jakich wartości x liczby 2, 2 sinx , cos2x są trzema kolejnymi wyrazami ciągu
geometrycznego?
16 cze 18:23
bezendu: @Karolina weź załóż sobie temat i tam zadawaj pytania
skorzystaj z tego b
2=ac
16 cze 18:24
mmk:
Odp: x=2
16 cze 18:25
Mila:
Jeśli zastosujesz zapis :
| a2 | | a3 | |
| = |
| , to bedzie prościej |
| a1 | | a2 | |
x+4≠0 z zał.
x
3+4x
2=10x+4
itd
16 cze 18:25
bezendu: Ok, a trzeba pisać jakieś założenia
16 cze 18:25
mmk:
Odp : była skierowana do bezendu
16 cze 18:26
bezendu: Dobra dziękuje, mam jeszcze jedno zadanko ale tym razem z wielomianów
16 cze 18:27
mmk:
Pisz jak rozwiązujesz
16 cze 18:28
bezendu:
Niech W(x)=x
2+mx+36
a) wyznacz te wartości parametru m, dla których równanie ma W(x)=0 ma dwa różne pierwiastki
dodatnie
| | W(x) | |
b) dla jakich wartości parametru m równanie |
| ma jeden pierwiastek ? |
| | x−4 | |
a)
założenia
Δ>0
a≠0
x
1*x
2>0
x
1+x
2>0
Δ=m
2−144
m
2−144>0
(m−12)(m+12)>0
m∊(−
∞,12)∪(12,
∞)
x
1*x
2>0
| 36 | |
| >0 36>0 i teraz co z tym |
| 1 | |
x
1+x
2>0
−m>0
m<0
cześć wspólna m∊(−
∞,12)
Δ=0
Δ=m
2−144
m
2−144=0
(m−12)(m+12)=0
m=12 lub m=−12
16 cze 18:35
mmk:
W a) błąd m€ (−∞, −12)
16 cze 18:42
Mila: a)m<−12
b) sprawdzam
16 cze 18:42
mmk:
W b) jeszcze sprawdź co będzie gdy x= 4
4
2+4m+36=0 ⇒ m= −13
to x
2−13x+36=0 ⇒ (x−9)(x−4)=0 ⇒ x= 9 −−− jedno rozwiązanie, bo x≠4
zatem Odp: m= {−13, −12, 12}
16 cze 18:46
mmk:
No to ja "spadam" ......... ( nie lubię "tłoku"
16 cze 18:46
bezendu: 4 dlatego że to jest podzielne przez 4, tak
16 cze 18:47
kulfon:
b) m = −12 bo m =12 jest poza dzieciną, m ∊ R \ {12}
a w a) chyba nic nie bedzie...
16 cze 18:47
bezendu: Dziękuje mmk
16 cze 18:47
Mila: b) m=12 lub m=−12 lub m=−13
16 cze 18:49
bezendu: Mila ale skąd się bierze to m=−13
jest to równanie więc zajmuję się tylko licznikiem...
16 cze 18:51
Mila:
Zobacz co napisała mmk− post 18:46'
Jeśli nie zrozumiesz, będę tłumaczyc.
16 cze 18:54
bezendu: właśnie zapytałem jej ale już uciekła
sprawdzam dla 4 bo to jest podzielne przez 4 ?
16 cze 18:55
Mila:
| | x2+mx+36 | |
Mamy równanie: |
| =0 |
| | x−4 | |
D=R\{4}
Badamy dla jakiego m równanie x
2+mx+36=0 ma dwa rozwiązania, a jednym z nich jest 4.
W(4)=4
2+4m+36=0
m=−13
sprawdzamy co wtedy się dzieje.
x
2−13x+36=0
Δ=169−144=25
| | 13−5 | | 13+5 | |
x1= |
| =4∉D odrzucamy lub x= |
| =9 zostaje jedno rozwiązanie. |
| | 2 | | 2 | |
16 cze 19:04
bezendu: Jednym z nich jest 4 dlatego że w mianowniku jest x−4 ? o to chodzi ?
16 cze 19:06
Mila: Tak, zobacz co zapisałam na początku.
To właśnie takie podchwytliwe zadanie.
16 cze 19:07
bezendu: Dziękuje, teraz już rozumiem
16 cze 19:10
Mila: Powodzenia w dalszych zmaganiach z Aksjomatem.
Jaką ocenkę dostaniesz na koniec roku?
16 cze 19:21
bezendu: Dziękuje, 4
Jutro cały dzień będę robił zadania z niego bo i tak do szkoły się nie idzie
16 cze 19:22
bezendu:
Ostatnie już zadanko na dziś
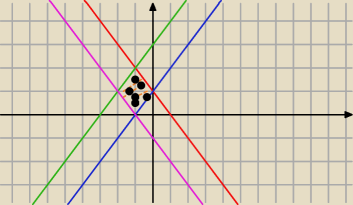
W układzie współrzędnych zilustruj zbiór punktów spełniający nierówność
|x+1|+|y−1|≤1
x≥−1 y≥1
x<0 y<1
1
0
x≥−1 i y≥1
x+1+y−1≤1
x+y+2≤1
y≤−x+1
2
0
x≥−1 i y<1
x+1−y+1≤1
−y≤−x−1
y≥x+1
3
0
x<−1 y≥1
−x−1+y−1≤1
y≤x+3
4
0
x<−1 i y<1
−x−1−y+1≤1
−y≤x+1
y≥−x−1
ok ?
16 cze 20:17
Mila: Ilustracja w porządku.
Zapis przypadków:
x+1≥0 i y−1≥0⇔x≥−1 i y≥1
x+1<0 i y−1<0⇔x<−1 i y<1 w tym masz usterkę.
reszta dobrze.
16 cze 20:30
bezendu: A jeszcze takie pytanie tego obszaru nad prostymi nie powinno się kreskować ?
16 cze 20:32
Mila:
Masz dobrze zaznaczyć obszar końcowy, pośrednie kroki? delikatnie można, ale całość będzie mało
czytelna, masz czas na wypracowanie skutecznej metody.
16 cze 21:02
bezendu: Dziękuje po raz kolejny za drogocenną wskazówkę
16 cze 21:13