Proszę o pomoc w tym zadaniu. Adrian: W trójkącie ABC mamy dane: |AC|=8, |BC|=12 oraz |∠ABC|=120 stopni. Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok Ab w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC

Mila: Sprawdź treść zadania.

Adrian: W trójkącie ABC mamy dane: |AC|=8, |BC|=12 oraz |∠ABC|=120 stopni. Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok AB w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC Treść zadania się zgadza. Proszę o pomoc

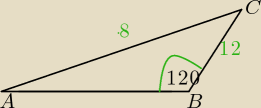
Mila: Zobacz, że nie mogą być takie dane, gdyż bok AC ma być najdłuższy w tym trójkącie. Sprawdź podane długości boków i oznaczenie kąta.

Adrian: W trójkącie ABC mamy dane: |AC|=8, |BC|=12 oraz |∠ACB|=120 stopni. Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok AB w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC Przepraszam tak powinno być

Mila: W trójkącie ABC mamy dane: |AC|=8, |BC|=12 oraz |∠ACB|=120 stopni. Przez wierzchołek C poprowadzono prostą prostopadłą do boku AB. Przecięła ona bok AB w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC

Adrian: tam zostaje BC

Mila: Dobrze, zaraz będę rozwiązywać.

Adrian: wielkie dzięki

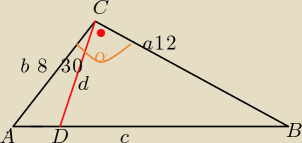
Mila: α=120⁰ a) w ΔACD:

	1		√3
PΔABC=		*8*12*sin120=48*		=24√3
	2		2

	1		1		1
PΔABC=		*8*d*sin30+		*d*12=4*d*		+6d=8d suma pól ΔADC i ΔDCB
	2		2		2

8d=24√3 d=3√3 b) z tw. cosinusów obliczymy c

	−1
c2=a2+b2−2*a*b*cos (1200), [ cos120=cos (180−60)=−cos60=		]
	2

	−1
c2=82+122−2*8*12*(		)
	2

c²=64+144+96 c²=304 c=√304=√16*19 c=4√19 Z tw, sinusów

c		4√19
	=2R⇔		=2R
sin120		√3   2

	4√57
R=
	3

Van Helsing: