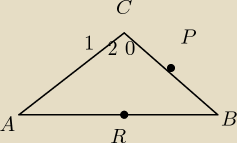
trojkat OoO: Obwod trojkata rownoramiennego ABC jest rowny (12+8√3) cm. Punkt P jest srodkiem odcinka BC, a punkt R dzieli odcinek AB w stosunku 3:2. Oblicz pole trojkata a) APC, b) ARC, c)PRB. (Pod C jest kat 120 stopni)

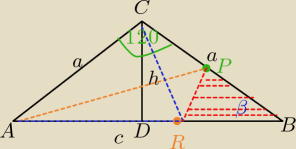
Mila: 2a+c=12+8√3 W Δ CDB:β=30⁰,

	DB		√3		DB
cos30=		⇔		=		⇔2|DB|=c=a√3
	a		2		a

2a+a√3=12+8√3 a(2+√3)=12+8√3 /*(2−√3) a*(4−3)=(12+8√3)*(2−√3) a=4√3 c=12

	1		1		1
PΔAPC=		PΔABC=		*		*4√3*4√3=
	2		2		2

Mila: Za szybko wysłałam cd. P_ΔARC |AR|=3x, BR=2x x− wspólna miara długości

	12
3x+2x=12⇔5x=12⇔x=
	5

	36
|AR|=
	5

	24
|BR|=
	5

	1		36		36
PΔARC=		*4√3*		* sin30=		√3
	2		5		5

	1		24
PΔPRB=		*		*2√3*sin30 dokończ
	2		5

OoO : wielkie dzięki, tam przy APC, jeszcze powinno być razy √3/2

OoO : A czy zamiast się rozpisywac na poczatku moglem odrazu wywnioskowac z obwodu (12+8√3), że podstawa czyli c to się rowna 12, a rowna się 4√3, bo wzor na obwod to podstawa plus 2a? czyli 12+2*4√3 ?

Mila: 18:45 , tak, opuściłam wartość sinusa, ( tak, to jest, gdy robi się skróty) Mogłeś (do 18:48)