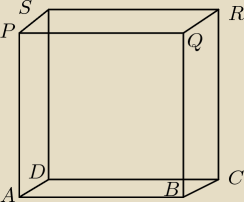
Dany jest sześcian, jak na rysunku. Długość krawędzi sześcianu jest równa 1. Od sześcianu
odcięto czworościany APQS oraz BQRP. Oblicz objętość otrzymanego wielościanu
(2
W trójkącie ABC punkt E należy do boku BC, punkt M jest środkiem odcinka AE. Proste AB
i MC przecinają się w punkcie F. Wykaż, że pole trójkąta MEC jest większe od pola trójkąta
MAF.
