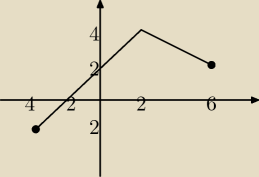
przekształć funkcje zyśka: Funkcja na wykresie to y=f(x). Jak należy przekształcić tą funkcję by otrzymać: a)y=−f(Ix−2I)

	1
b)y=		f(IxI=2)
	2

c)2−f(I−3+xI) Zapisz odpowiednie przekształcenia.

PW: a) trochę nietypowe. Zazwyczaj widząc argument (x−2) rutynowo przesuwamy dziedzinę (a z nią wykres) w prawo o 2 − żeby to x−2 dało sie obliczyć. Tutaj tzeba ostrożniej, bo widzimy wartość bezwzględną: |x−2|. Należy zastanowić się, jakie można brać x, aby f(|x−2|) dała się obliczyć. Odpowiedź jest prosta: |x−2| musi należeć do dziedziny funkcji f, to znaczy do przedziału <−4,6>.. Należy więc rozwiązać nierówność −4≤|x−2|≤6. Żeby nie zanudzać − rozwiązaniem jest zbiór x∊<−4. 8>. Dziedzinę już mamy, teraz pytanie o wartości funkcji g(x)=f(|x−2|). Dla x∊<−4,2> liczby |x−2| przebiegają przedział między 6 a 0 "od prawej do lewej", a więc wykres funkcji g na przedziale <−4,2> jest obrazem wykresu funkcji f(x) z przedziału <0, 6> w symetrii o osi OY, przesuniętym o 2 w prawo, tak aby "zaczynał się" w punkcie o pierwszej współrzędnej −4. Dla x∊(2, 8> liczby |x−2| przebiegają przedział (0, 6>, a wiec wykres funkcji g na przedziale (2,8> jest wykresem funkcji f z przedziału (0, 6> przesuniętym o 2 w prawo. To była "łopatologia", a praktyczny sposób wynikający z tych może niezbyt udanych rozważań jest taki, że: a) wykres funkcji f leżący nad przedziałem <0,6> przesuwamy o 2 w prawo, a następnie b) wykres uzyskany w punkcie a) przekształcamy przez symetrię o osi x=2. Uzyskany w punktach a) i b) wykres funkcji g(x) = f(|x−2|) przekształcamy symetrycznie względem osi OX uzyskując szukany wykres funkcji −g(x) = −f(|x−2|).