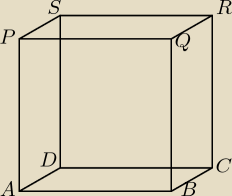
(1 Pawexs: Dany jest sześcian, jak na rysunku. Długość krawędzi sześcianu jest równa 1. Od sześcianu odcięto czworościany APQS oraz BQRP. Oblicz objętość otrzymanego wielościanu (2 W trójkącie ABC punkt E należy do boku BC, punkt M jest środkiem odcinka AE. Proste AB i MC przecinają się w punkcie F. Wykaż, że pole trójkąta MEC jest większe od pola trójkąta MAF.

Pawexs: .

Pawexs: Chociażby mała wskazówka proszę

Pawexs: Pomocy

Karko: Eh...

wredulus_pospolitus: 1) znasz objętość sześcianu jak również długości jego ścian odcinane są czworościany z podstawą długości √2 i ścianami bocznymi długości 1 wyznacz ich objętości ... różnica to szukana wartość

Karko: A więc jak tam drugie ? :x

wredulus_pospolitus: Karko −−− chociaż to narysuj ... jest prawie północ ... nie mam siły sobie tego wyobrażać

Bogdan: Sprawdź Pawexs treść zadania, nie twierdzę, że podana przez Ciebie treść jest niedokładna, ale upewnij się, że czworościany są takie, jak podałeś. Spróbuj narysować tę bryłę.