Pochodne
Agata: Witam jak wyznaczyć przedziały w których funkcja jest malejąca np. f(x)=4x
3+20x
2?
Obliczyłam pochodną ale nie wiem co dalej

14 cze 18:35
Mila: f'(x)<0 to funkcja jest malejąca
f'(x)>0 to funkcja jest rosnąca
14 cze 18:38
Agata: f'(x)=12x2+40x czyli muszę obliczyć nierówność kwadratową i będzie przedział x ∊(−40/12, 0)
14 cze 19:05
Agata: A jak sprawdzić czy istnieją punkty ekstremalne funkcji f(x)?
14 cze 19:10
Milan:
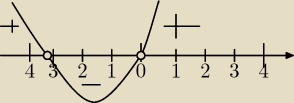
f'(x)>0⇔
12x
2+40x>0 /:4
⇔
3x
2+10x>0
x(3x+10)>0
| | 1 | |
Dla x∊(−∞,−3 |
| ) ∪(0,∞) funkcja jest rosnąca |
| | 3 | |
| | 1 | |
Dla x∊(−3 |
| ,0) funkcja malejąca |
| | 3 | |
f'(x)=0⇔
Przy przejściu przez miejsca zerowe pochodna zmienia znak
| | 1 | | 2000 | |
x=−3 |
| (↗↘) ma maksimum ymax= |
| |
| | 3 | | 27 | |
x=0 (↘↗) ma minimum y
min=0
14 cze 19:24
Agata: Ok wielkie dzięki
To jeszcze zapytam, bo nie jestem pewna czy dobrze rozumuję, mam następnie obliczyć
charakterystykę monotoniczności to liczę drugą pochodną funkcji f i podstawiam 0 i −313.
I tak dla 0 będzie 10>0minimum, zaś dla −313 <0 maksimum
14 cze 19:32
Mila:
Ja inaczej ustalam typ ekstremum, ( popatrz na strzałki w nawiasie), ale możesz ze znaku
drugiej pochodnej.
14 cze 19:50
Agata: Ok, a jak teraz mam ustalić czy funkcja posiada asymptoty, bo pionowa to którą wyrzucamy z
dziedziny, a pozioma?
Sorki że tak Was męczę ale to moje być albo nie być

14 cze 19:54
Agata: Pomoże ktoś z tymi asymptotami, proszę

14 cze 20:42
14 cze 20:55
Agata: dzięki wielkie

14 cze 21:40
Agata: Nie wiem czy wiecie ale ratujecie ludziom życie

14 cze 21:50
Mila: To miło, nie wszyscy uważają za stosowne napisać nam dobre słowo.

Powodzenia.
Jestem, mozesz zadawać pytania.
14 cze 21:54
Agata: Dzięki wysłałam kolejne pytanko ale w nowej zakładce
14 cze 21:57

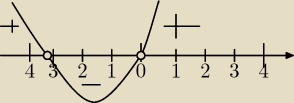 f'(x)>0⇔
12x2+40x>0 /:4
⇔
3x2+10x>0
x(3x+10)>0
f'(x)>0⇔
12x2+40x>0 /:4
⇔
3x2+10x>0
x(3x+10)>0




 Powodzenia.
Jestem, mozesz zadawać pytania.
Powodzenia.
Jestem, mozesz zadawać pytania.