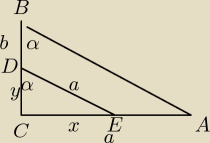
Rozgryzienie trójkątów podobnych Cornik: Błagam niech mi ktoś pomoże rozgryźć te zadania bo naprawde niewiem jak sie za nie zabrać proooooosze 1) Suma pól dwóch podobnych trójkątów prostokątnych jest równa 169 cm². Znajdź pole każdego z tych trójkątów jeżeli trójkąty są podobne w skali k = 5/12 2) W trójkącie prostokątnym ABC poprowadzono odcinek DE równoległy do przeciwprostokątnej AB tak że D należy do BC i E należy do AC. Długość tego odcinka jest równa długości przyprostokątnej AC, kąt przeciwległy tej przyprostokątnej ma mairę alfa. Oblicz stosunek pola trójkąta DEC do pola trojkąta ABC.

AS: Zadanie 1

	5
Jeżeli trójkąty są w skali liniowej k =		to stosunek pól tych trójkątów
	12

	25
jest równy k2 =
	144

P + k²*P = 169

	25
P +		P = 169
	144

144*P + 25*P = 144*169 169*P = 144*169 |: 169 P = 144 Pole pierwszego trójkąta wynosi P1 = 144 Pole drugiego trójkąta wynosi P2= 25 (144*25/144) Zadanie 2 (rys) ΔCDE: x = a*sin(α) y = a*cos(α) PΔCDE = 0.5*x*y = 0.5*a*sin(α)*a*cos(α) = 0.5*a²*sin(α)*cos(α) ΔABC

b
	= ctg(α) ⇒ b = a*ctg(α)
a

PΔABC = 0.5*a*b = 0.5*a*a*ctg(α) = 0.5*a²*ctg(α) Stosunek pól trójkątów

	PΔCDE		0.5*a2*sin(α)*cos(α)
k =		=
	PΔABC		0.5*a2*ctg(α)

	sin(α)*cos(α)		sin(α)*cos(α)
k =		=		= sin2(α)
	ctg(α)		cos(α)/sin(α)