Wykresy funkcji trygonometrycznych technick: Jak narysować takie wykresy: a) f(x) = sinx + |sinx|

	|cosx|
b) f(x) =
	cos

use: normalnie z definicji wartosci bezwzględnej rozpisz te przyklady w drugim bedzie albo 1 a;bo −1 a w pierwszym 2sinx albo 0

6-latek: tu masz b)

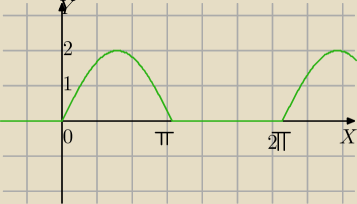Mila: a) f(x) = sinx + |sinx| 1) |sinx|=sinx dla sinx≥0⇔dla x∊<0+2kπ,π+2kπ> Wtedy mamy wzór f(x)=sinx+sinx=2sinx 2) |sinx|=−sinx dla sinx<0 ⇔dla x∊(π+2kπ,2π+2kπ) f(x)=sinx−sinx f(x)=0 funkcja stała.

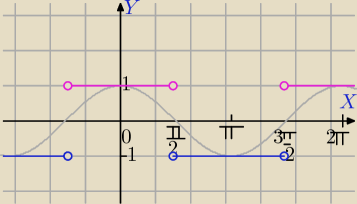Mila: Zadanie 2)

	|cosx|
f(x)=		i cosx ≠0
	cosx

|cos(x)|=cosx dla cosx>0 ( patrz wykres pomocniczy−popielaty)

	π		3
dla x∊(0+2kπ,		+2kπ) ∪(		π+2kπ,2π+2kπ)
	2		2

	cosx
f(x)=		=1
	cosx

	π		3π
f(x)=−1 dla x∊(		+2kπ,		+2kπ)
	2		2